Цифровые логические микросхемы
Мы разобрались, как сконструировать логические вентили из отдельных транзисторов, и даже попрактиковались в этом на макетной плате. Можем двигаться дальше. Как вы уже видели на примере вентиля Исключающее ИЛИ, с помощью дискретных приборов, даже на большой макетной плате, не получится собрать ничего пригодного для прикладных, а не учебных задач. Время перейти к изучению микросхемам цифровой логики.
- что кроется за «серийностью» логических микросхем
- как выглядят DIP-микросхемы и в чем их особенность
- что делать, если нам нужна микросхема 3ИЛИ, а в наличии есть только 2ИЛИ
- какие логические преобразования существуют
Серии и назначение микросхем цифровой логики
Внутри одного корпуса микросхемы может находиться несколько десятков, а иногда и сотен транзисторов, которые образуют сразу несколько логических вентилей. Это удобно, несмотря на то, что мы уже не получаем доступа к внутренним узлам схемы — только к ее входам и выходам.
Микросхемы цифровой логики изготавливают в виде серий с определенными обозначениями. Что вообще кроется за словом «серия» в микроэлектронике:
- Тип логики. В нашем курсе по схемотехнике мы рассматриваем только КМОП-устройства, но знайте, что есть множество других микросхем — ТТЛ, ТТЛШ, ЭСЛ, И2Л и прочие.
- Совместимость. Даже внутри одного типа микросхем бывают подгруппы, отличающиеся по разным параметрам. Поэтому микросхемы из разных серий могут взаимодействовать друг с другом не очень хорошо, иногда даже конфликтовать. А вот внутри одной серии микросхемы прекрасно подходят для работы друг с другом.
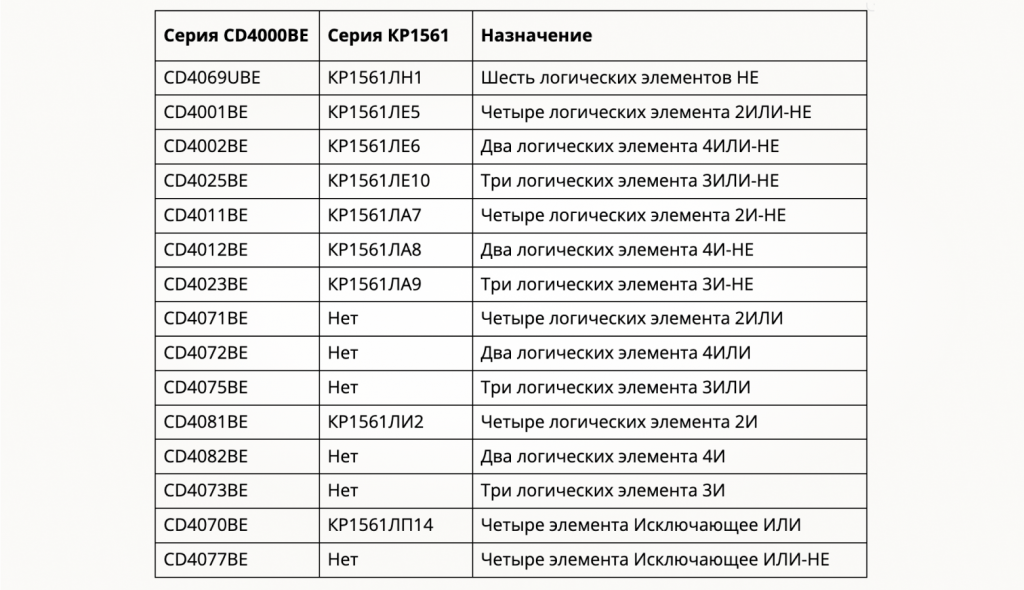
Для наших опытов будем использовать известную серию КМОП-микросхем — CD4000BE (отечественный аналог — КР1561). Нули после четверки в зарубежном названии каждой микросхемы заменяются цифровым кодом, который указывает на ее функциональное назначение. В отечественной серии функциональное назначение и подтип микросхемы кодируются двумя буквами и одной или двумя цифрами, которые пишутся после «КР1561». Некоторые наиболее часто применяемые из них приведены в таблице:
При соединении микросхем выходного тока одной из них достаточно, чтобы при необходимости переключать транзисторы сразу в нескольких подобных микросхемах. Или светодиод зажечь. А вот для управления чем-то более мощным понадобится усилитель сигнала — например, на дискретном МОП-транзисторе.
Напряжение питания КМОП серии CD4000BE может меняться в широком диапазоне — от 5 до 15 вольт. Поэтому все устройства в нашем курсе будут получать питание от батарейки «Крона» на 9 вольт.
Микросхемы серии CD4000BE заключены в двухрядные корпуса DIP (dual in-line package) — будто жучки на ножках.

Давайте внимательно посмотрим на картинку выше. На одной из коротких сторон прямоугольного корпуса есть выемка (часто она полукруглая) — это ключ, обозначающий первый вывод. Если расположить микросхему ключом вверх, то нумерация выводов будет начинаться слева от него и продолжаться против часовой стрелки. Как правило, самый последний вывод — это плюс питания, а вывод, расположенный по диагонали, на противоположной стороне, — минус.
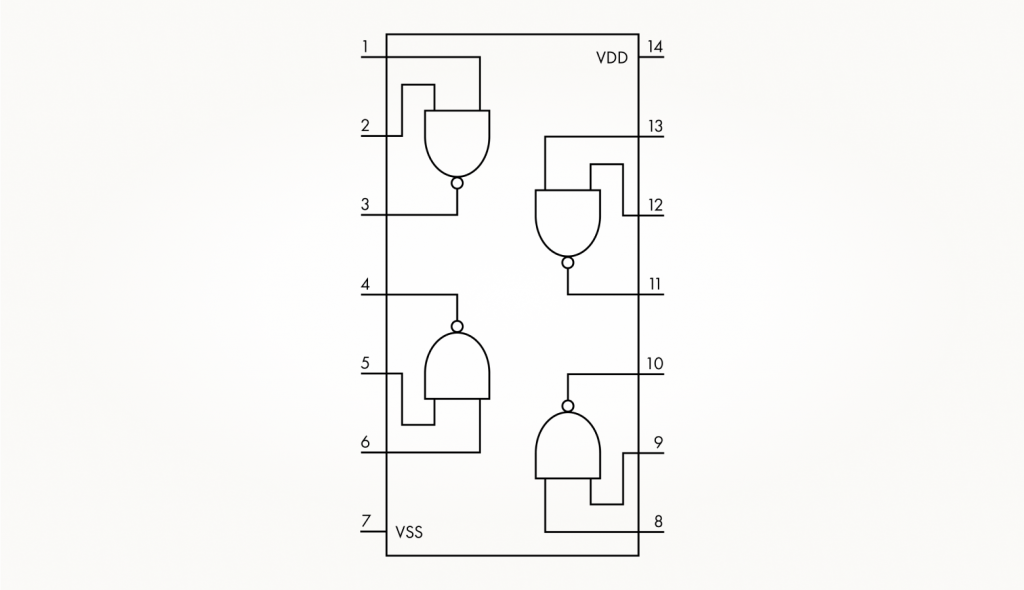
На рисунке ниже — условное размещение четырех вентилей 2И-НЕ внутри корпуса микросхемы CD4011BE. Условное потому, что сам полуповодниковый кристалл со всеми четырьмя вентилями внутри корпуса занимает совсем мало места строго по центру. А к выводам подключается проводочками внутри корпуса. В справочной литературе традиционно VDD обозначают вывод для подключения плюса питания, а VSS — для подключения минуса. То же самое назначение выводов справедливо и для микросхем CD4001BE, CD4071BE, CD4081BE, СD4070BE, СD4077BE с учетом другого типа вентиля внутри микросхем, конечно же.
На макетной плате DIP-микросхема располагается так, чтобы два ряда выводов были по разные стороны от канавки посередине платы. Нередко предостерегают, что КМОП-компоненты можно необратимо повредить разрядом статического электричества — например, если коснуться пальцами выводов микросхемы. Проскочившая искра может создать разность потенциалов в пару киловольт, и это приведет к пробою затворного диэлектрика и к выходу МОП-транзистора из строя. Поэтому выводы микросхемы пальцами лучше лишний раз не трогать.
На практике, впрочем, с такими повреждениями встречается не каждый: входы современных микросхем защищают от разрядов статического электричества.
Но лучше все же не тестировать качество выбранной микросхемы и проявить разумную осторожность. Если вы сомневаетесь в работоспособности того или иного вентиля, обращайтесь к таблицам истинности, индикаторам и данным о расположении входов и выходов микросхемы. И, конечно же, убедитесь, что к ней подключено питание.
Приступаем к опытам с микросхемами
В качестве первого эксперимента над микросхемами посмотрим, что произойдет с вентилями И-НЕ и ИЛИ-НЕ (CD4011BE и CD4001BE, соответственно), если их входы замкнуть между собой. В таблице истинности схемы исчезнут все строки, в которых входные сигналы разные, и останутся только две: «все нули» и «все единицы».
При этом оба типа вентилей, независимо от количества входов, превратятся в обычные инверторы. Знание, что инвертор можно получить объединением входов И-НЕ или ИЛИ-НЕ, позволяет более гибко использовать элементную базу. Например, если на плате находится одна из таких микросхем, а в ней есть свободный вентиль, то можно не применять логический элемент НЕ из шести, входящих в состав CD4069UBE (см. таблицу выше), а задействовать уже установленные компоненты. И хотя каждая из примененных микросхем содержит по четыре вентиля своего типа, в нашем эксперименте мы задействовали по одному из них — остальные не потребовались. Выводы, которые соответствуют полностью неиспользованным логическим элементам, можно оставлять неподключенными.
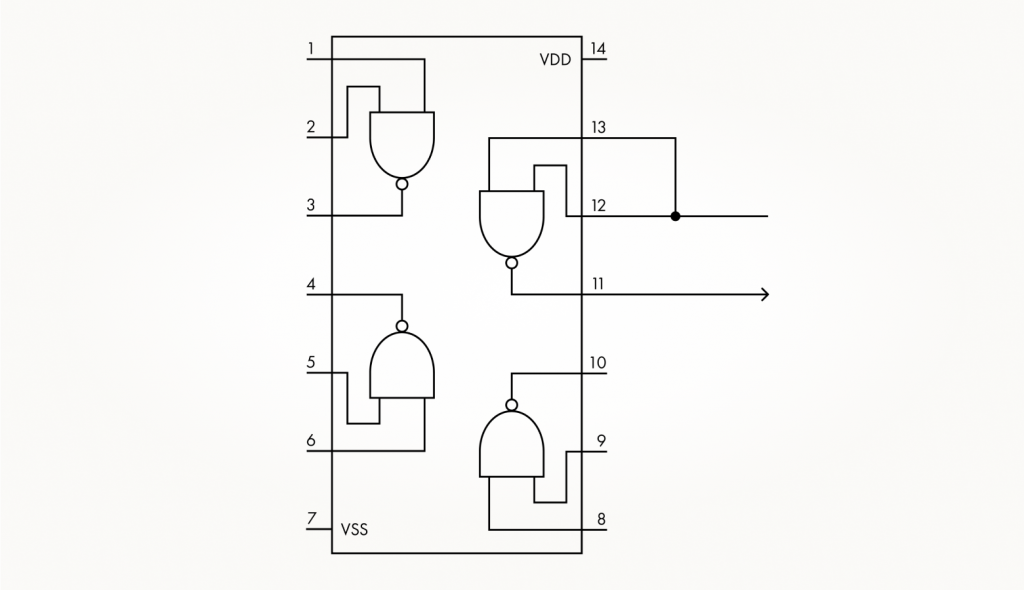
В предыдущем тексте мы рассмотрели принципы построения многовходовых вентилей на транзисторах. Существуют и логические микросхемы с элементами, у которых от двух до четырех входов. Но что делать, если нужна микросхема 3ИЛИ, а в наличии есть только 2ИЛИ? Внутрь не проникнуть, транзисторы в микросхемы не добавить (в этом они принципиально отличаются от схем на дискретных элементах).
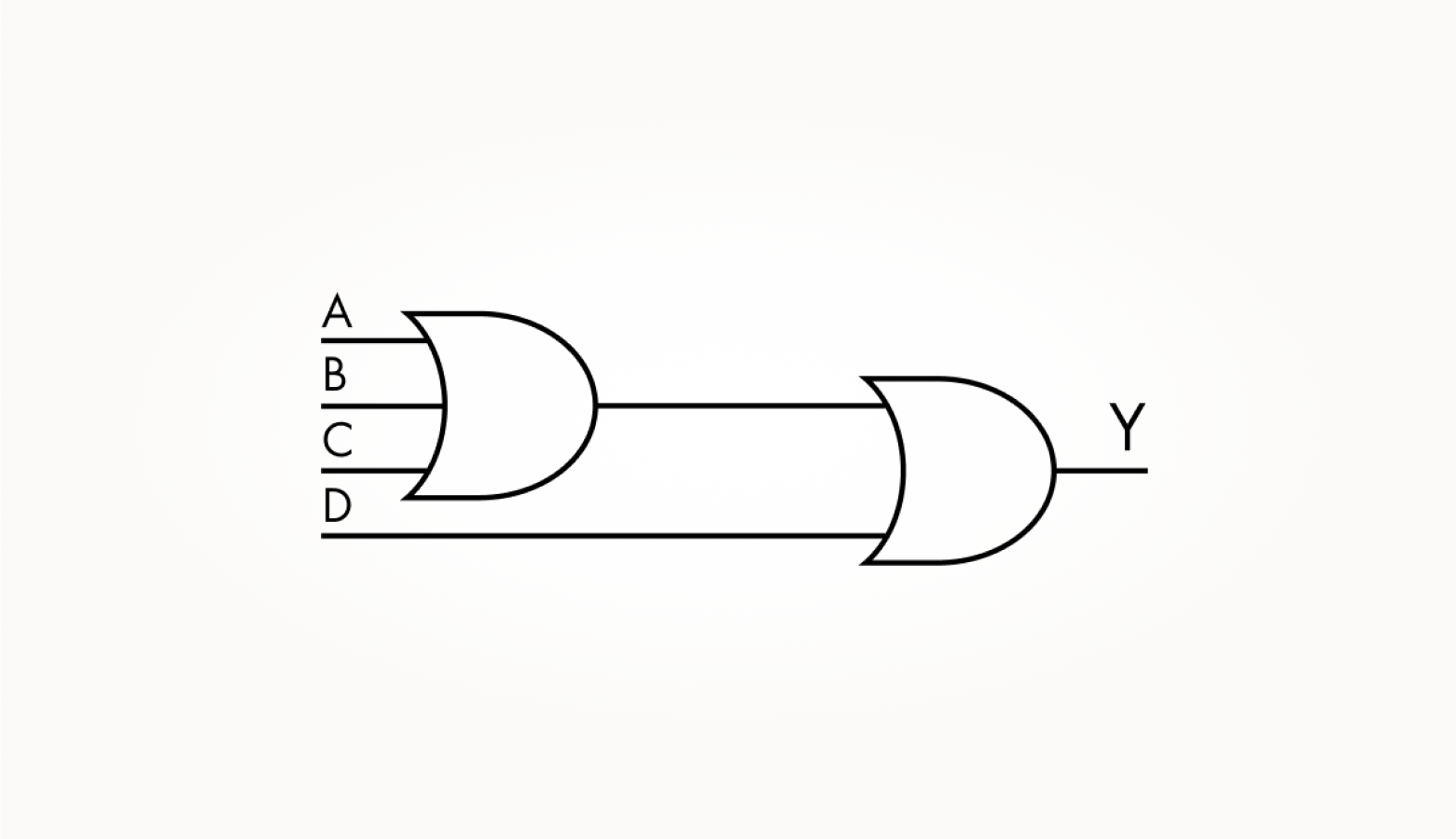
Для увеличения числа входов можно соединять элементы в каскады вентилей, следующих друг за другом. В таких случаях говорят, что применяется каскадирование. Если с помощью операции ИЛИ объединить сначала два входа, а потом добавить к ним третий с помощью того же ИЛИ, мы получим тот же эффект, что и от применения ИЛИ ко всем трем входам сразу. Посмотрите на схеме, как из двух вентилей 2ИЛИ можно получить 3ИЛИ.
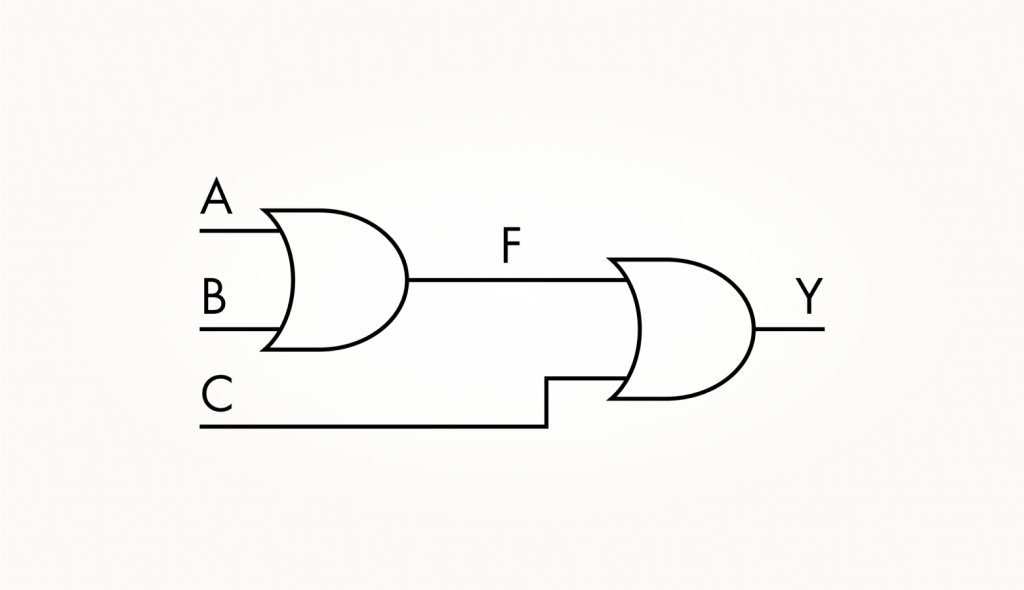
Промежуточный сигнал, который обозначается буквой F, будет равен нулю только в том случае, если нули поданы на входы A и B. В свою очередь, выходной сигнал Y будет нулем, только если и F, и C равны нулю. Поэтому такая схема по выполняемой функции: Y = F + C = A + B + C — соответствует вентилю 3ИЛИ. При этом, в каком именно порядке подключать сигналы к схеме, значения для логики ее работы не имеет.
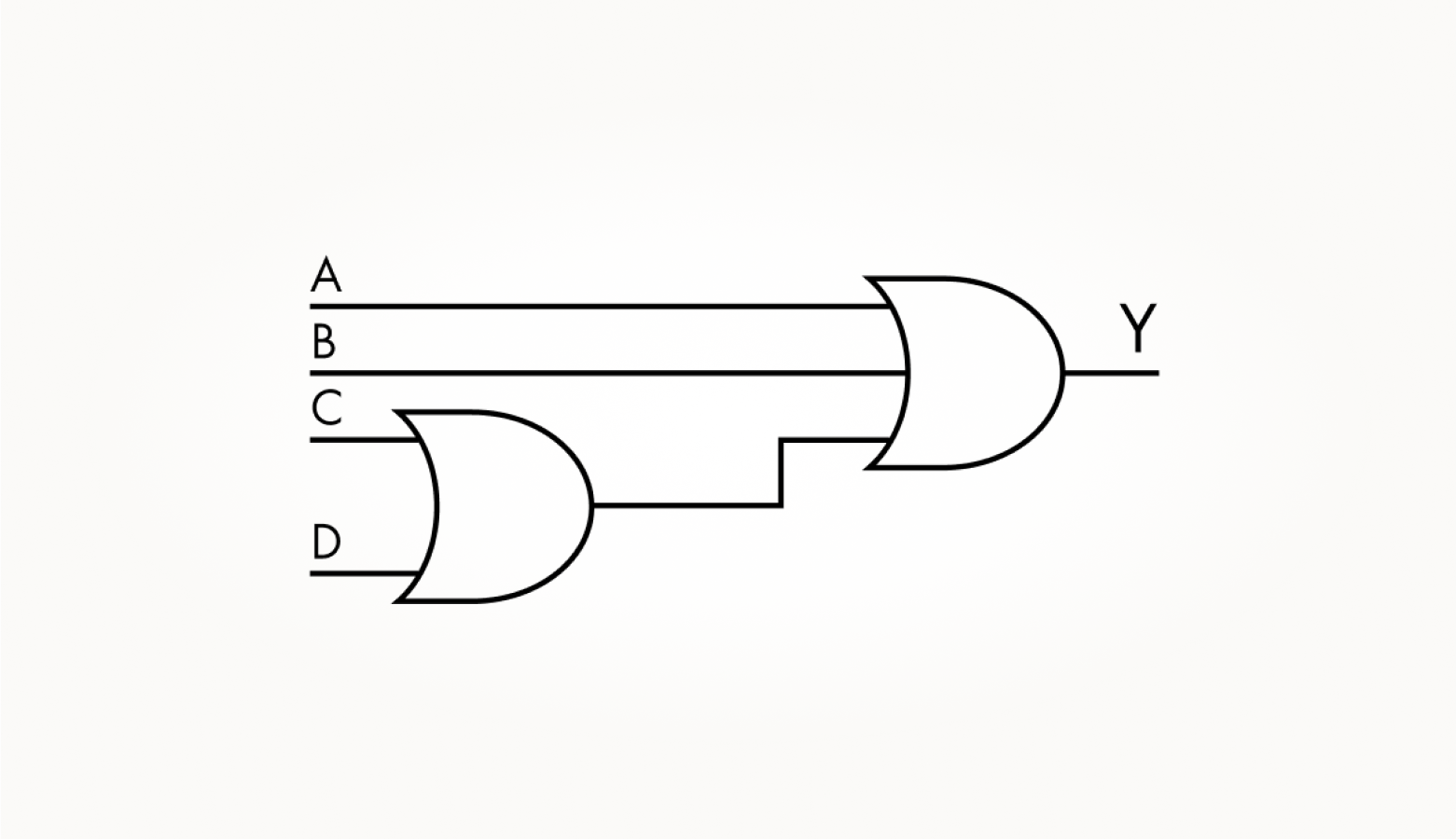
Точно так же из трех вентилей 2ИЛИ микросхемы CD4071BE нетрудно получить, например, 4ИЛИ. Как показано на схеме ниже.
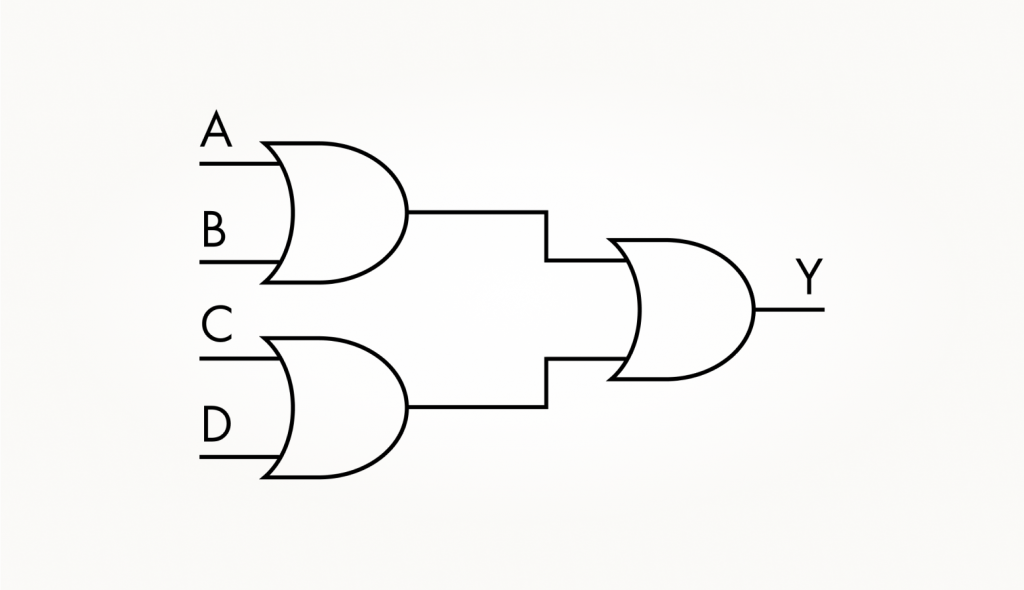
Вентиль 4ИЛИ также легко конструируется из одного 2ИЛИ и одного 3ИЛИ двумя способами.
1. Составьте схему получения 4И из нескольких вентилей 2И.
2. Составьте схему получения 3И из нескольких вентилей 2И.
Правильные ответы вы найдете в конце статьи.
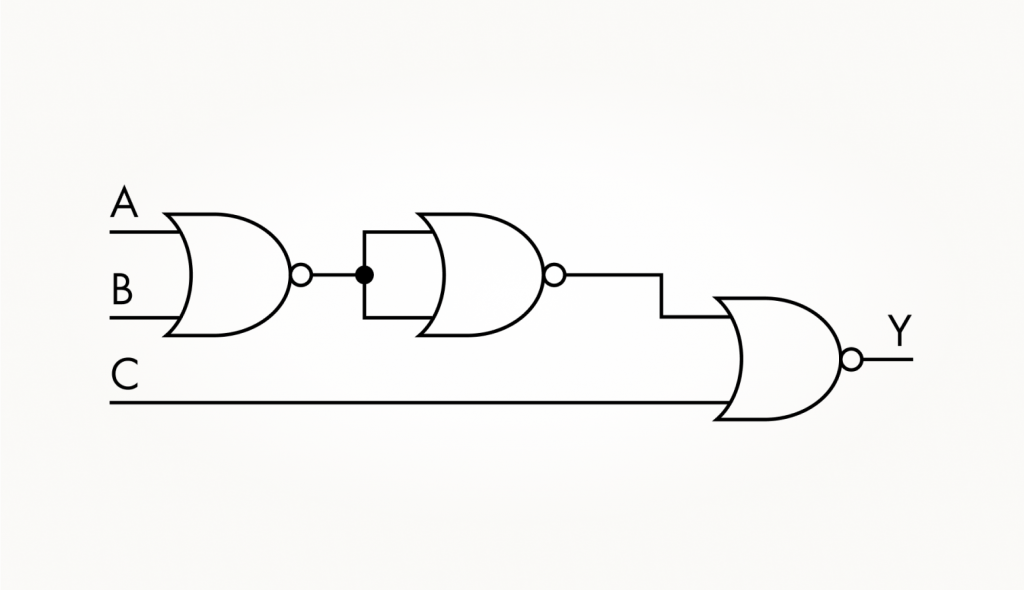
Добавить входы в элементы И-НЕ и ИЛИ-НЕ с помощью одноименных вентилей будет сложнее. Например, как сконструировать 4И-НЕ из 2И-НЕ? Трех вентилей 2И-НЕ недостаточно. А если поставить их по каскадной схеме, как мы делали для 4И, то на входы второго каскада сигналы придут инвертированными. Таблица истинности такой схемы будет соответствовать элементу, попарно объединяющему входы по И, а потом — результаты для каждой пары по ИЛИ. Вы можете проверить нас, составив таблицу истинности и перебрав все возможные 16 состояний схемы, приведенной ниже.
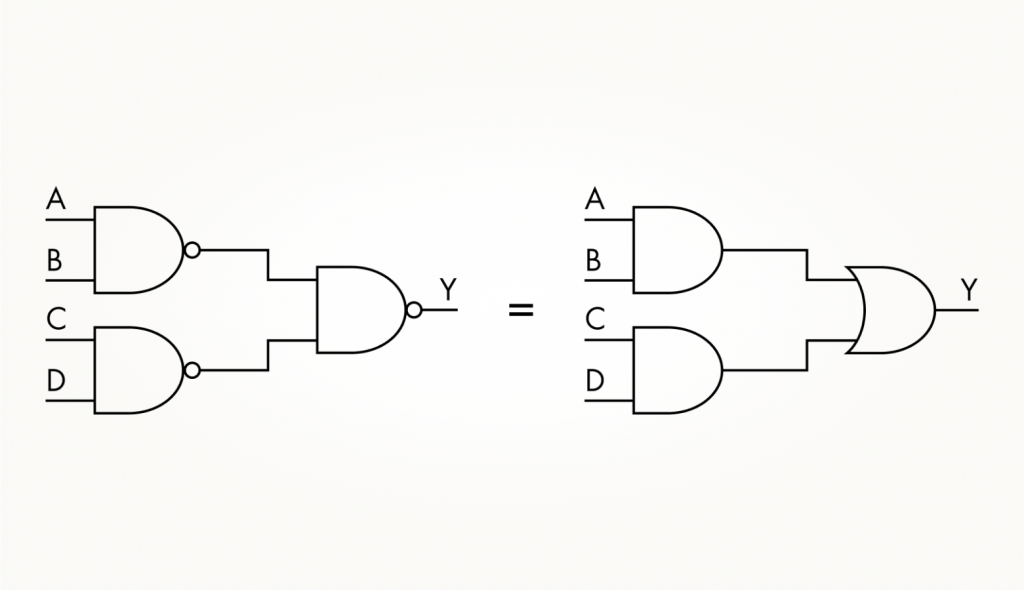
Знание булевой алгебры и формул преобразования двоичных выражений позволяет обойтись без больших таблиц истинности. Но метод с таблицами очень наглядный, используется наравне с формулами, так что навык составления таблиц очень вам пригодится. Мы будем активно применять его уже в следующих материалах курса. Так, при создании сложных схем из множества вентилей полезно проверять ее логическую функцию с помощью таблицы истинности.
Итак, для создания 4И-НЕ нам необходимо нейтрализовать инверсию выходов вентилей, образующих первый каскад обработки сигналов. Для этого придется между имеющимися каскадами добавить еще один, промежуточный, состоящий из инверторов.
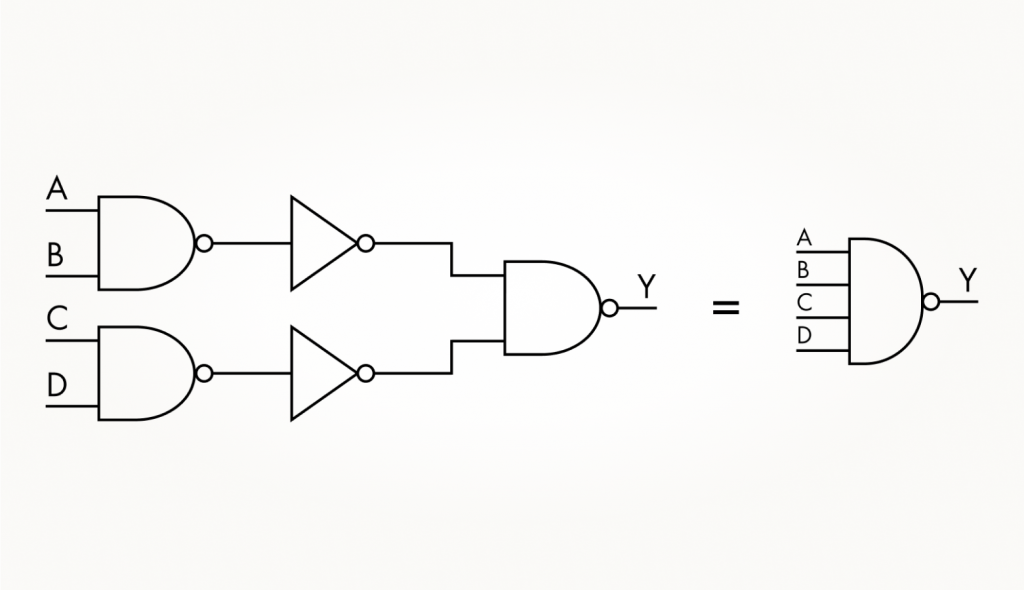
3. Составьте схему получения 4ИЛИ-НЕ только из 2ИЛИ-НЕ.
4. Составьте схему получения 3ИЛИ-НЕ только из 2ИЛИ-НЕ.
Другой очевидный вариант построения многовходовых И-НЕ и ИЛИ-НЕ — собрать аналогичные по числу входов вентили И или ИЛИ, а затем добавить инвертор на выход.
Как видите, существует масса способов добиться требуемого результата с помощью ограниченного набора микросхем. Это удобно и позволяет в ряде случаев не добавлять лишние компоненты на плату. Для этого надо лишь немного разобраться в правилах преобразования функций в двоичной логике.
Можно ли не задействовать входы или выходы?
Бывает, в одном корпусе остаются неиспользованными не целые вентили, а только часть их входов. Например, микросхема CD4072BE состоит из двух ИЛИ с четырьмя входами. А нам требуется трехвходовой вентиль, но его нет под рукой. Как поступить?
Тут нужно знать, что неиспользуемые входы КМОП-логики должны быть присоединены к одному из используемых входов или к какому-то полюсу питания. Если их никуда не подключить, неизвестно, какой потенциал будет у затвора транзистора на этом входе в процессе работы, как вы уже знаете из предыдущих материалов.
Поэтому лишние входы используемых вентилей не должны, как говорят инженеры, «болтаться в воздухе». Вопрос лишь в том, какой сигнал на них нужно подать, чтобы не нарушить логическую функцию. Так, например, если свободный вход упомянутой микросхемы CD4072BE подключить к единице, то на выходе в соответствии с таблицей истинности ИЛИ получить ноль никак не получится. А с логикой на основе операции И ситуация прямо противоположная. Поэтому у вентилей И и И-НЕ неиспользованные входы обязательно должны быть привязаны к логической единице, а у ИЛИ и ИЛИ-НЕ, соответственно, к нулю. Здесь не нужен никакой резистор, можно подключить их непосредственно к питанию.
Другой способ решения проблемы лишних входов — подать какой-то из входных сигналов не на один, а на несколько входов сразу. В этом случае возрастет нагрузка на источник сигнала, но отрицательно это повлияет лишь в быстродействующих применениях, то есть не в наших схемах. Поэтому вы во всех примерах из нашего курса можете использовать тот способ, который окажется наиболее удобным для вас.
С выходами КМОП-схем все проще: их можно оставлять неподключенными без всяких последствий. Сейчас мы рассматриваем простые вентили с одним выходом, но в дальнейшем познакомимся с более сложными элементами, где выходов несколько и часть из них не используются.
Некоторые логические преобразования
Мы уже упоминали ранее, что двойная инверсия сигнала равна самому сигналу. Это же правило справедливо для комбинации сигналов. Вообще, в дискретной математике и двоичной логике существует целый набор строго доказанных правил преобразования логических выражений. Они помогают более гибко подходить к конструированию нужных вам устройств из минимального набора логических вентилей и не загромождать плату корпусами микросхем. Если вы не знакомы с ними, то рекомендуем сперва изучить ролик на полях, чтобы двигаться дальше с пониманием тех преобразований, которые мы будем применять.
Наиболее часто применяемые из набора преобразований — это правила де Моргана, названные так в честь доказавшего их математика. Они есть в ролике на полях, но давайте рассмотрим их отдельно:
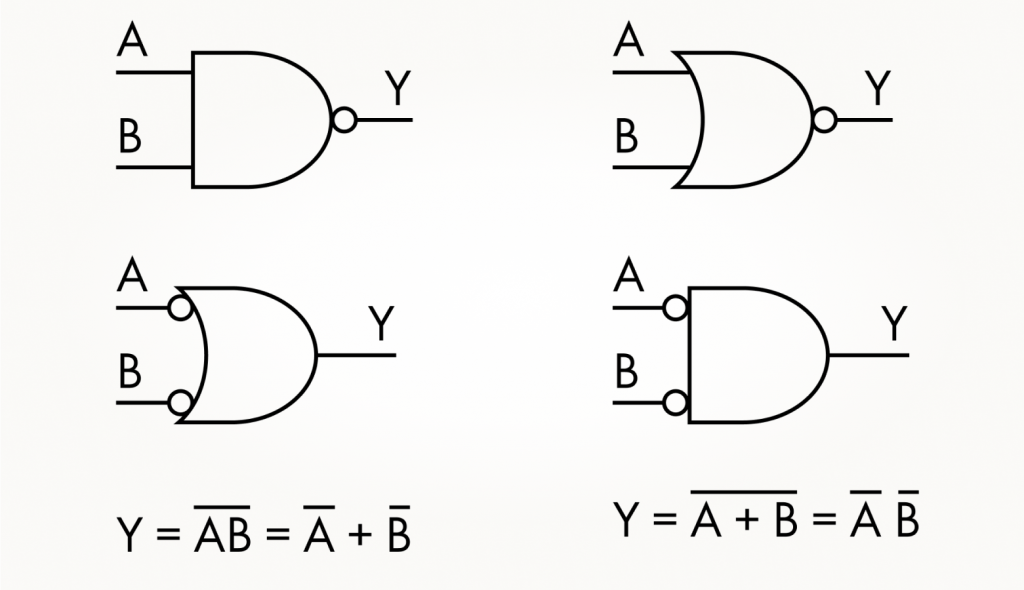
Получается, вентили И-НЕ и ИЛИ-НЕ — это универсальные элементы, из которых можно построить любую логическую функцию! Ведь и правда, инвертор из каждого из них можно получить простым объединением входов. Соответственно, И из двух И-НЕ получить элементарно, как и ИЛИ из двух ИЛИ-НЕ, добавив на выход «обычного» вентиля еще один «закороченный». На схеме выше показано, как по правилам де Моргана И-НЕ преобразуется в ИЛИ с инверсией на входах и наоборот. Есть и вариант получения Исключающего ИЛИ из этих вентилей — их потребуется сразу несколько штук, но, тем не менее, это возможно.
Про вентили, из набора которых можно создать любую логическую функцию, говорят, что они образуют функционально полный набор, или логический базис. Вот такой базис можно создать всего из одного вентиля И-НЕ или ИЛИ-НЕ по выбору. А вот к И или ИЛИ нужно еще добавить инвертор, чтобы набор стал функционально полным.
Неудивительно, что именно микросхемы И-НЕ или ИЛИ-НЕ наиболее часто применяются в схемах цифровой логики и популярны до сих пор.
Самостоятельное творчество
На рисунке ниже — графические обозначения элементов из так называемой «библиотеки стандартных ячеек». Это набор из всех необходимых «кирпичиков» для создания цифровых схем. При разработке микроэлектроники разнообразие элементов очень велико. Используются не только простые вентили, с которыми вы уже познакомились (они в первой строке рисунка), но и более сложные. Мы пока не упоминали многие из них, но скоро это исправим.
Обратите внимание на сложносоставные элементы из логических вентилей с конца пятой строки до начала последней. Выберите любой из них, поймите по его изображению его логическую функцию, составьте таблицу истинности и попробуйте реализовать выбранный элемент на любых микросхемах из серии CD4000BE.
Вы можете назначить удобную вам нумерацию входов. Кружочек возле входа, как и кружочек на выходе, означает инверсию. На первых порах удобнее всего просто заменить кружок на входе обычным инвертором, чтобы не ошибиться при составлении таблицы истинности.
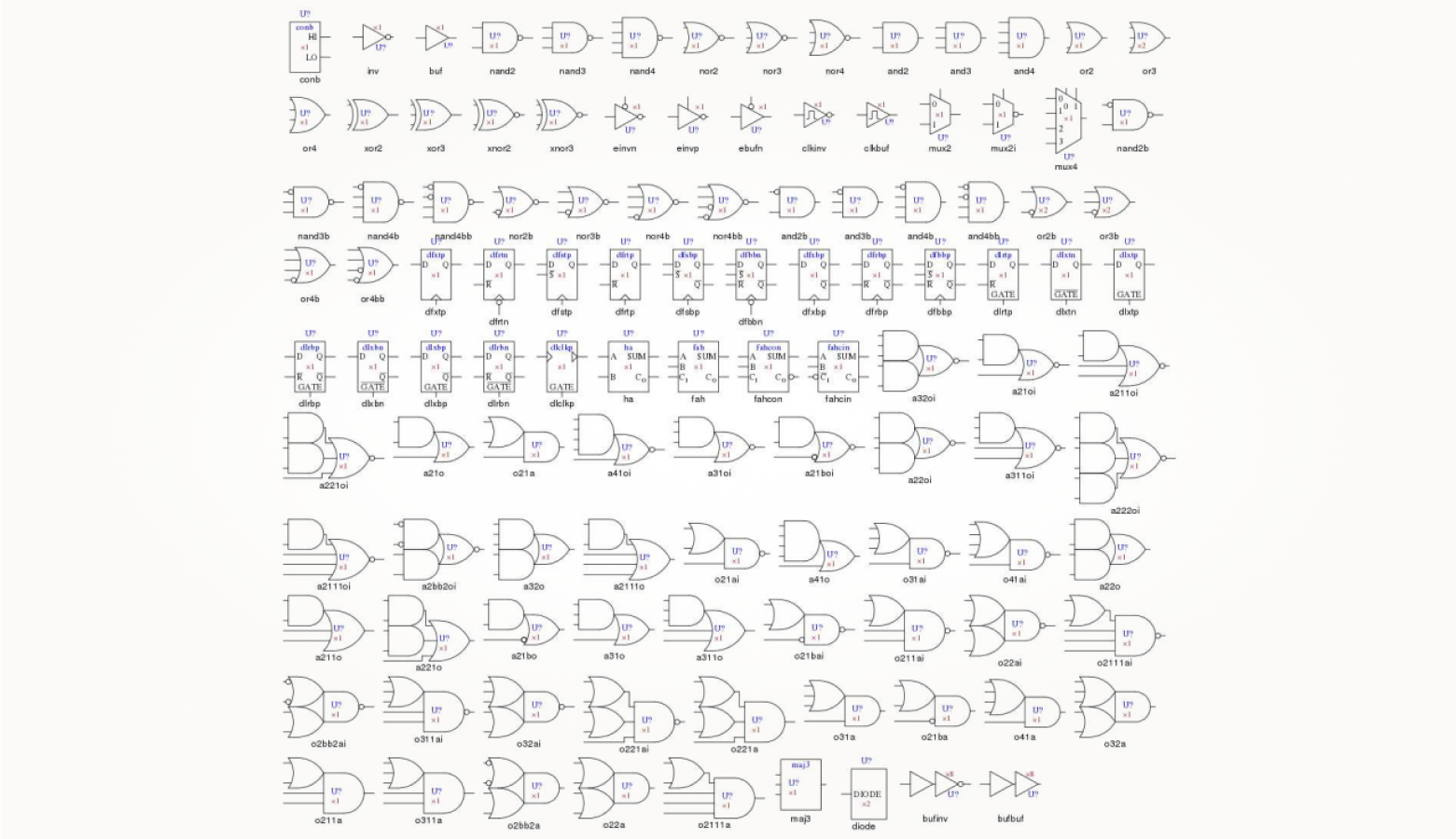
Для примера рассмотрим решение такой задачи для второго справа вентиля в пятом ряду, обозначив для удобства его входы и промежуточные узлы, как показано на рисунке:
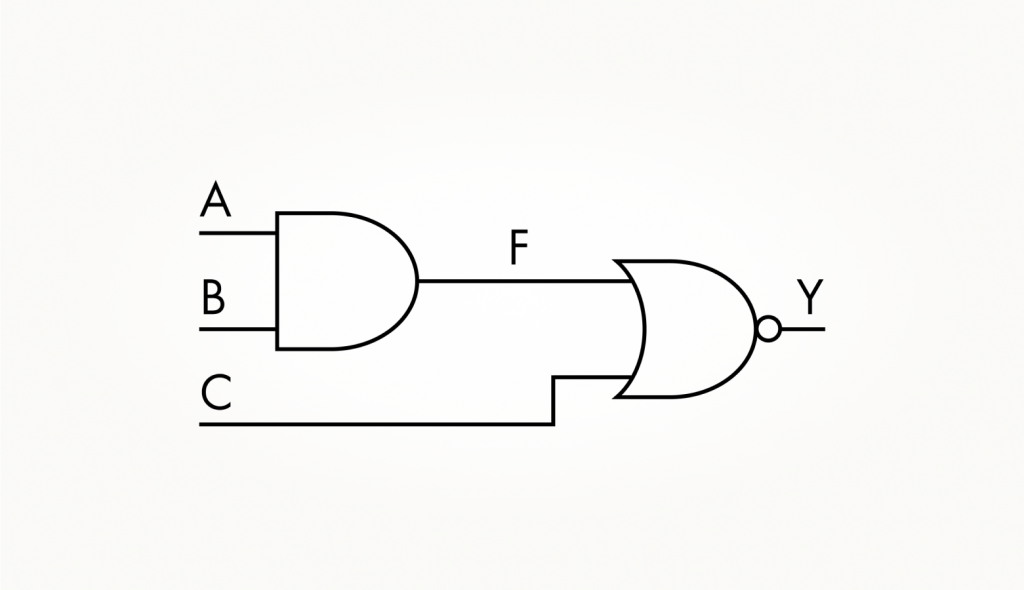
Его логическая функция будет при таких обозначениях записана в следующем виде:
Как мы видим, она просто отражает в текстовом виде то, что изображено на схеме: вентиль логическое И соответствует операции умножения, логическое ИЛИ — сложения, а инверсия обозначается чертой над тем выражением, которое на схеме дано с кружочком.
Таблица истинности здесь выглядит вот так:
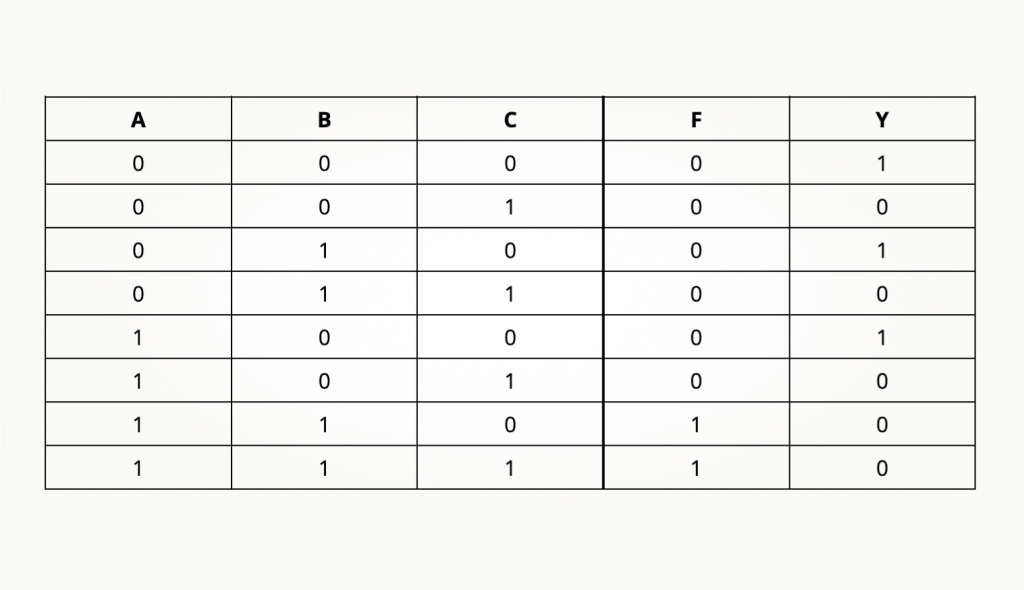
А уж со сборкой на макетной плате этого простого элемента из двух вентилей проблем не будет. После этого можно простым перебором всех 8 вариантов сочетаний входных сигналов убедиться «в железе» в правильности решения на бумаге.
Таким же образом можно проверить свои силы и знания на любом другом сложносоставном вентиле из предложенных. Удачи вам!
Ответы на вопросы для самопроверки
1. Схема получения 4И из нескольких вентилей 2И.
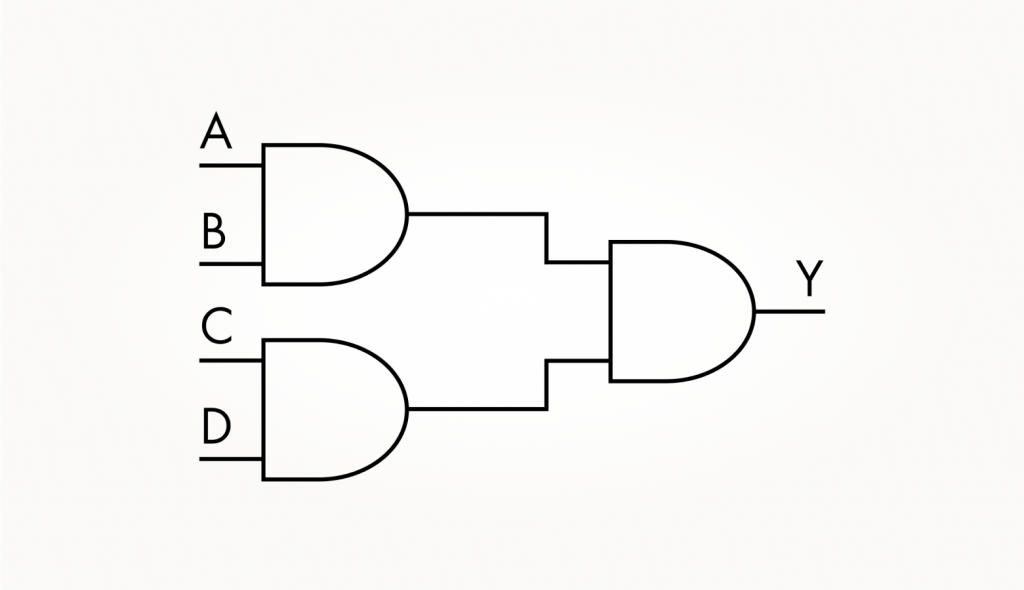
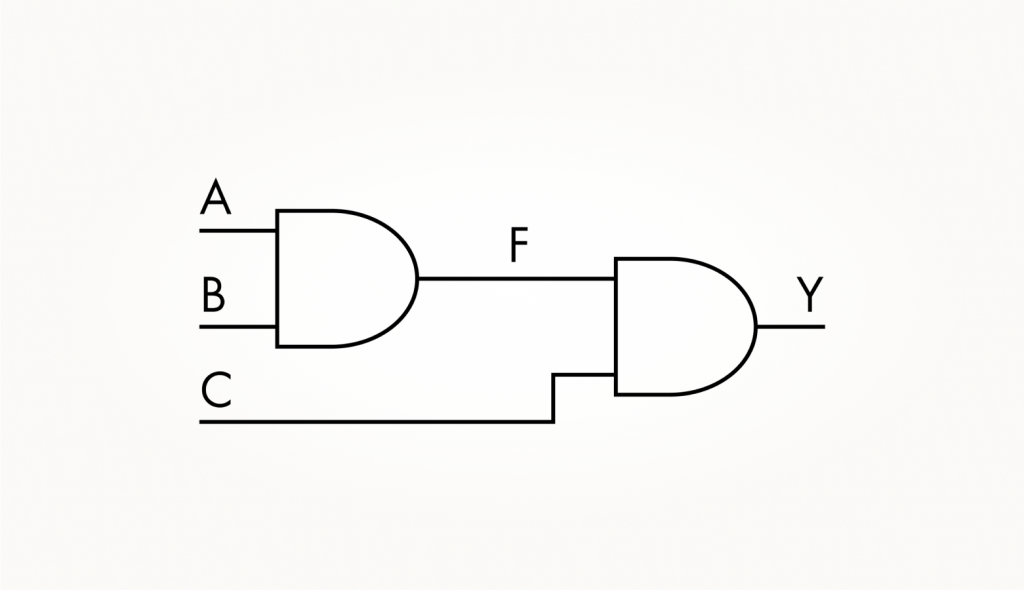
2. Схема получения 3И из нескольких вентилей 2И.
3. Схема получения 4ИЛИ-НЕ только из 2ИЛИ-НЕ.
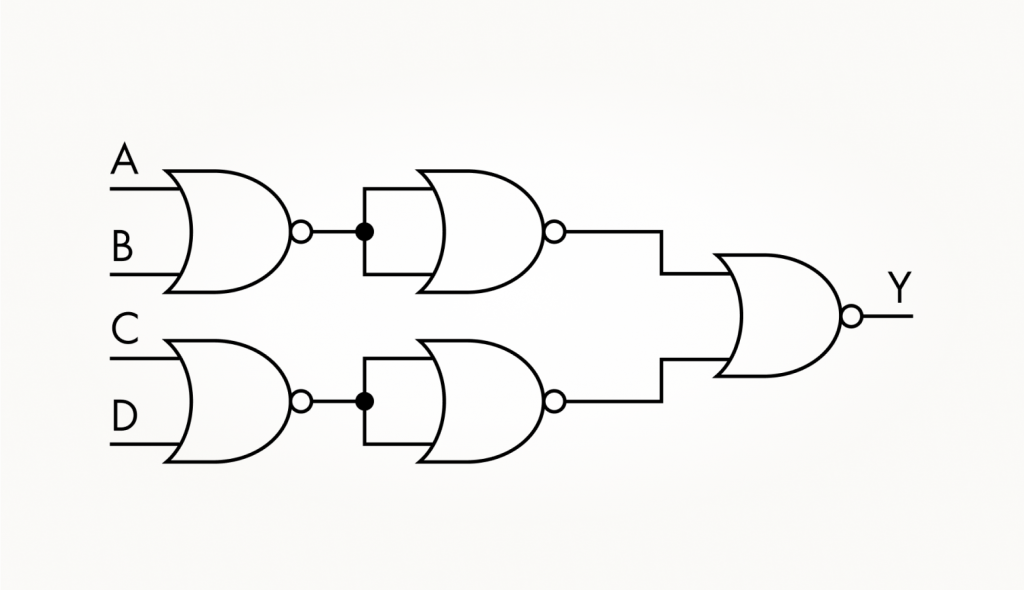
4. Схема получения 3ИЛИ-НЕ только из 2ИЛИ-НЕ.