Погружение в матрицу: расширение RISC-V от T-Head

Продолжим «антологию матричных расширений» текстом про независимое матричное расширение RISC-V от компании T-Head.
Почему мы рассматриваем именно его? Интересно понять, что из себя представляет будущее стандартное матричное расширение RISC-V, попробовать реализовать алгоритм с его использованием, соотнести это со своим предыдущим опытом низкоуровневых оптимизаций. Кроме того, это интересная возможность попробовать написать программу для расширения, которого еще нет ни в одном процессоре, и запустить ее на эмуляторе.
А еще ISA этого расширения весьма минималистична и идеально подходит для тех, кто никогда не использовал матричные расширения в своем коде, но хочет попробовать (или узнать, как это выглядит изнутри). Текст не требует опыта низкоуровневых оптимизаций математических библиотек: погружение в матрицу будет постепенным.

Интро про T-Head RVM
Вспомним, что мы узнали из предыдущего текста. T-Head RVM — это независимое матричное расширение RISC-V. В базовой комплектации (без Sparsity Subset, который сейчас активно разрабатывается) содержит восемь двумерных матричных регистров, которые используются и для сомножителей, и для аккумуляторов. Длина строки регистра равна RLEN бит, а число строк определяется как RLEN/32. Число столбцов зависит от ширины элементов матрицы и равно RLEN/N бит, где N — ширина элемента.
Расширение находится в стадии разработки, плат с его реализацией пока нет. Тем не менее, доступна эмуляция расширения на QEMU: можно попробовать запустить код, написанный под это матричное расширение, сравнить с векторной или скалярной реализацией алгоритма, получить опыт программирования под него.
ISA расширения достаточно легковесна: содержит порядка 20 инструкций. Это инструкции для:
- умножения блоков матриц и аккумуляции,
- прочих операций над матрицами (список таких операций T-Head сейчас расширяет),
- загрузки и выгрузки данных из матричных регистров,
- копирования данных между регистрами разного типа,
- конфигурирования матричных регистров, их освобождения
и т. д.
В статье мы разберем эти инструкции, а также соответствующие им интринсики, и рассмотрим их особенности.
Репозиторий
Спецификацию расширения, демо-приложения и другие полезные вещи вы можете найти в репозитории. Вы можете склонировать его себе для дальнейшей работы. У репозитория следующая структура:
Для быстрого запуска демо-приложений необходимо выполнить два скрипта из папки demos:
После запуска будут сформированы логи с подробной статистикой по инструкциям, вызовам функций
Хочу обратить внимание, что репозиторий содержит библиотеку shl. Это высокопроизводительная библиотека гетерогенных вычислений от T-Head. Среди ее исходников вы можете найти ассемблерные реализации алгоритмов с использованием матричного расширения и C-реализации алгоритмов с использованием интринсиков векторного расширения. Если хотите углубиться в тему низкоуровневых оптимизаций математических библиотек, советую их изучить. Это может быть полезно для обучения и вдохновения при написании своих реализаций алгоритмов.
Далее мы детально разберем особенности конфигурирования матричных регистров, API интринсиков Кроме того, соотнесем интринсики со спецификацией инструкций для тех, кто любит использовать ассемблерные вставки.
Спецификация
Сначала рассмотрим, какие типы данных поддерживаются, и договоримся об обозначениях. На данный момент расширение допускает работу:
- с целочисленными типами, как со знаком, так и без него, шириной от 8 до 64 бит,
- с числами с плавающей точкой шириной от 16 до 64 бит.
В таблице ниже приведены используемые в репозитории обозначения. Типу данных <dtype>_t в API интринсиков соответствует аббревиатура <atype>, а в названиях инструкций ширина элемента обозначается суффиксом <sbit>.

Префикс «m» в названии типа говорит о том, что это не скаляр, а матрица: так, тип m<dtype>_t соответствует одному матричному регистру, элементы которого имеют тип <dtype>_t. Для чисел с плавающей точкой в названии матричных типов вам может встретиться постфикс «x2»: m<dtype>x2_t — это объединение двух матричных регистров, элементы которых имеют тип <dtype>_t.
Кроме того, в названиях матричных типов вы можете встретить постфикс «v»: m<dtype>v_t — это обозначение вектора в матричном регистре. В текущей реализации такому типу данных соответствует непосредственно матричный регистр и номер строки внутри него.
Теперь перейдем к операциям, которые мы можем выполнять.
Конфигурирование матричных регистров
При использовании матричного расширения начинаем мы всегда с конфигурирования матричных регистров под те размеры матричных блоков M, N и K, с которыми нам предстоит работать. При этом надо учитывать, что архитектура накладывает ограничения на максимальное число строк и столбцов в регистре:
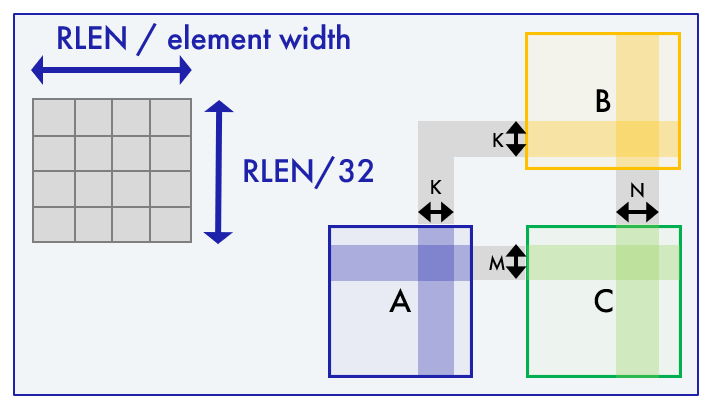
Если разработчик попытается сконфигурировать регистры с превышением этих ограничений, они будут сконфигурированы по максимально возможным значениям размерностей. Поэтому инструкции конфигурирования возвращают 32-битное число с описанием получившейся конфигурации:
- Первые 8 бит этого числа соответствуют значению M (это число строк в блоках первого сомножителя, матрицы A, и аккумулятора — матрицы C),
- Следующие 8 бит — это N (число столбцов в блоках второго сомножителя, матрицы B, и аккумулятора — матрицы C).
- Последние 16 бит — это k = K * element width, где K — число столбцов в блоке первого сомножителя, матрицы А, и строк в блоке второго сомножителя, матрицы B.
Последний момент необходимо запомнить и учитывать при конфигурировании регистров.
Вы можете сконфигурировать все три размерности разом, передав число в описанном выше формате в следующий интринсик:
B случае конфигурирования размерности K не забывайте, что задавать надо не K, а k = K * element width:
Соответствуют этим интринсикам конфигурирования отдельных размерностей следующие инструкции:
Например, если мы хотим сконфигурировать матричные регистры для случая M = N = K = 4 и dtype = float32, то мы можем выполнить следующее:
После этого вы можете проверить значение mnk, чтобы узнать, удалось ли сконфигурировать регистры желаемым образом.
Загрузка данных
Вы сконфигурировали матричные регистры. Теперь нам необходимо загрузить в них данные. Здесь возможны два варианта.
Первый вариант — у вас в памяти находится большая матрица, из которой вам нужно загрузить блок в матричный регистр. Помимо указателя на первый элемент блока, вам потребуется передать в интринсик загрузки еще и stride, который равен числу элементов в строке матрицы, умноженному на их ширину:
Этому интринсику соответствует следующая инструкция:
Например, для корректной загрузки блока по указателю block_b с размером, соответствующим конфигурации матричного регистра, из матрицы с элементами типа float и числом столбцов ROW_SIZE, необходимо выполнить:
Второй вариант — размер вашей матрицы соответствует конфигурации регистра. Например, вы работаете с небольшими матрицами или алгоритм предусматривает предварительную подготовку блоков в буферах соответствующего размера. Тогда вы загружаете всю матрицу в регистр:
Данному интринсику соответствует следующая инструкция:
Вы можете вспомнить, что для матриц с элементами типа float16.64 спецификация предусматривает сдвоенные матричные регистры (немного терпения: тайна их предназначения будет раскрыта в следующем подразделе). Для них также доступна загрузка из матрицы соответствующего размера:
Последнему интринсику соответствует инструкция:
Выгрузка данных
Точно так же для выгрузки данных из матричных регистров у нас есть два варианта: выгрузка блока в большую матрицу и в матрицу соответствующего размера.
В первом случае нам снова необходимо указывать stride, значение которого определяется, как описано выше:
Здесь ms — матричный регистр, из которого необходимо выгрузить данные, а base — указатель на первый элемент блока внутри большой матрицы. Для рассмотренного выше примера загрузки блока выгрузка данных обратно в тот же блок будет иметь вид:
Соответствующая инструкция выглядит так:
Во втором случае, когда выгрузка данных из регистра производится в буфер соответствующего размера, используется следующий интринсик:
При реализации на ассемблере для этих целей используйте команду:
Для матриц с элементами типа float16.64 также доступна выгрузка данных из сдвоенного матричного регистра в буфер соответствующего размера:
Соответствует этому следующая инструкция:
Матричное умножение
Перейдем к наиболее интересной операции — умножению блоков матриц. Для нее в API интринсиков есть существенные особенности, и проще начать не с них, а непосредственно с инструкции:
Здесь происходит умножение двух блоков матриц из двух матричных регистров ms1 и ms2, а также добавление их произведения к содержимому третьего матричного регистра, md, с сохранением в него же. У элементов матриц — тип float<sbit>. Какие здесь есть подводные камни? Во-первых, матрицу B, согласно документации, необходимо предварительно транспонировать, то есть инструкция выполняет следующее:
Таким образом, в регистре ms2 находится блок размером не K \times N элементов, а N \times K. Кроме того, выше уже упоминалось о том, что есть ограничения на максимальное число строк и столбцов в матричном регистре. А в случае матричного умножения у нас еще и взаимосвязаны размеры блоков операндов и аккумулятора, что накладывает дополнительные ограничения. С учетом всего перечисленного получаем следующие максимальные значения размеров блоков при умножении матриц с элементами типа float16.64:
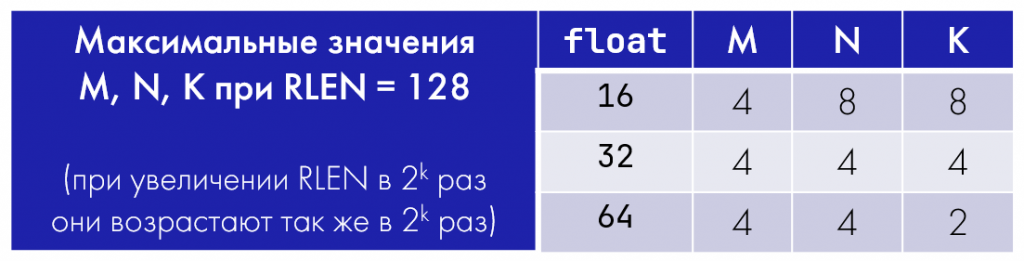
И вот здесь есть интересный момент.
В случае чисел с плавающей точкой одинарной точности все понятно и прекрасно. Максимальные значения M, N и K равны, а значит, все три блока — и сомножители, и аккумулятор — имеют один и тот же размер, 4\times4. И у нас один матричный регистр приходится на плитку матрицы А, один — на плитку матрицы В, один — на плитку матрицы С.
А вот в случае элементов с половинной или двойной точностью у нас возникает более интересная конфигурация: появляются блоки разных размеров. Например, для float16 у блока матрицы A размер M \times K = 4 \times 8. Блок матрицы C такого же размера (M \times N), что в случае float16, как видно из таблицы выше, также соответствует размеру 4 \times 8. Однако размер блока матрицы B от них отличается: N \times K = 8 \times 8.
Возникает естественный вопрос: как это соотнести с тем, что остальные регистры вмещают блоки 4 \times 8? На самом деле, достаточно просто. Это означает, что для блока матрицы В нам необходимо использовать два регистра 4 \times 8, и в сумме они дадут 8 \times 8. Собственно, для этого и требуются упоминаемые выше сдвоенные регистры.
По этой причине API интринсиков для умножения матриц выглядит не так просто, как соответствующая инструкция: в интринсиках необходимо указывать, для каких операндов требуются сдвоенные регистры. Напоминаю, что в таких типах данных у нас появляется постфикс «x2» после <dtype>, а у интринсиков следующий вид:
Матричное умножение с увеличением ширины аккумулятора
Казалось бы, с умножением матриц с элементами типа float16.64 мы разобрались. Но в рассмотренном случае элементы аккумулятора и сомножителей были одного и того же типа, то есть имели одинаковую ширину. Однако во многих задачах для получения результатов с приемлемой погрешностью при использовании половинной или одинарной точности для элементов матриц-сомножителей требуется использовать более широкие аккумуляторы. Поэтому спецификация матричного расширения T-Head содержит инструкцию для умножения матриц с элементами типа float16 или float32 и аккумуляцией результата в матрицу с элементами типа float32 или float64 соответственно, то есть с увеличением ширины аккумулятора в два раза:
Отличие от названия предыдущей инструкции — в букве «w» (widen).
Из-за того что ширина элементов матрицы C теперь в два раза больше ширины элементов матриц A и B, ограничения на конфигурацию матричных регистров отличаются от тех, что были в предыдущем случае. В итоге получаем следующие ограничения на максимальные значения M, N и K в зависимости от типа элементов матриц-сомножителей:
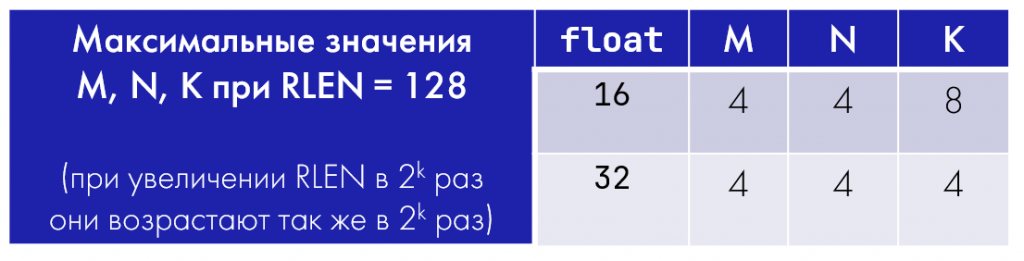
Как и в предыдущем случае, в интринсиках необходимо указывать, для каких операндов требуются сдвоенные регистры:
С умножением вещественных матриц мы разобрались. Теперь перейдем к умножению целочисленных матриц.
Матричное умножение целочисленных матриц
Матричное расширение T-Head позволяет выполнять такую операцию для сомножителей с 8-битными или 16-битными элементами. При этом для целочисленного умножения в T-Head RVM аккумулятор всегда шире в четыре раза по сравнению с сомножителями, в названии соответствующих команд это подчеркивается буквой «q» — quarter. Поэтому ограничения на максимальные значения M, N и K в зависимости от типа элементов матриц-сомножителей отличаются от рассмотренных выше случаев:
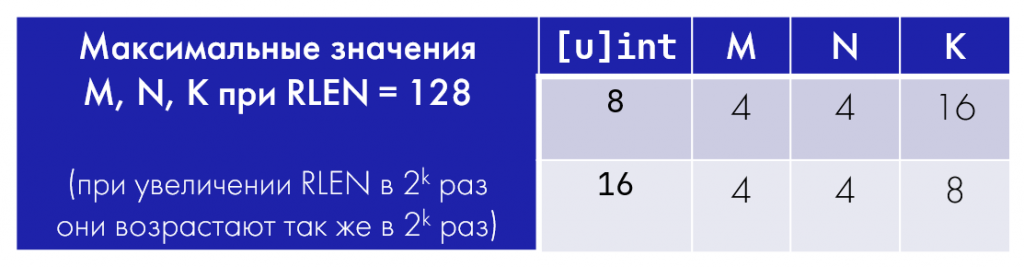
Проанализировав таблицу, можно сделать вывод, что в случае целочисленного умножения матриц с 16-битными элементами для аккумулятора нам потребуется сдвоенный матричный регистр. Если тип элементов обеих матриц-сомножителей знаковый либо, наоборот, беззнаковый, API интринсиков следующий:
Соответствует этим функциям инструкция:
Если же тип элементов матрицы B беззнаковый, а матрицы A — нет, то необходимо использовать функции:
На ассемблере им соответствует следующая инструкция:
Если же наоборот, элементы матрицы, А беззнаковые, а B — нет, то для их умножения используем функции:
Инструкция в этом случае следующая:
Поэлементные операции
Теперь рассмотрим более простые в плане конфигурирования регистров операции — поэлементные. Пока их можно производить только для матриц с элементами типа <dtype> = int{32,64}.
Поэлементное сложение. Вы можете поэлементно сложить элементы из двух матричных регистров и результат сохранить в третий матричный регистр:
Также можно к каждой строке матричного регистра прибавить строку с номером index из другого матричного регистра:
Кроме того, можно к каждому элементу матричного регистра прибавить одно и то же число:
Перечисленным операциям поэлементного сложения соответствуют следующие инструкции:
Поэлементное вычитание. Операция происходит аналогично, с той лишь разницей, что «add» в названиях интринсиков меняется на «sub»:
Таким образом, мы можем вычитать матрицу из матрицы, строку матрицы из каждой строки другой матрицы и одно и то же число из каждого элемента матрицы. С инструкциями тоже все аналогично:
Поэлементное умножение. Думаю, теперь разобраться с назначением интринсиков для этой операции ни для кого не составит труда:
Точно так же, как и с соответствующими им инструкциями:
Тем не менее, по сравнению с поэлементным сложением и вычитанием у поэлементного умножения есть одна особенность.
Поэлементный арифметический сдвиг вправо. В этой операции второй операнд, задающий сдвиги, всегда беззнаковый. Вы можете задавать целую матрицу сдвигов, и к каждому элементу будет применяться свой сдвиг:
Можно задать строку сдвигов, и этот вектор будет применяться к каждой строке матричного регистра:
Кроме того, можно указать в качестве сдвига только одно число. Тогда для каждого элемента матрицы будет выполнен сдвиг на указанное число бит:
Вышеперечисленным интринсикам для поэлементного арифметического сдвига вправо соответствуют следующие инструкции:
Напомню, что арифметический сдвиг вправо, например на 1 бит, выглядит следующим образом:
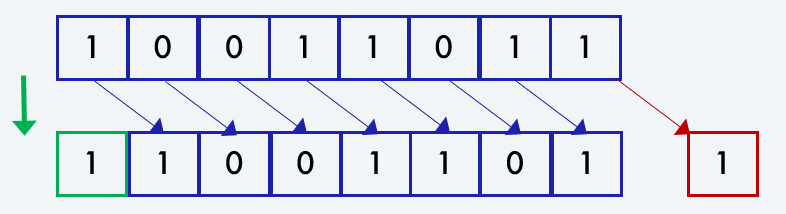
Копирование данных
С поддерживаемыми матричными операциями мы разобрались. Теперь — о копировании данных между регистрами.
Для копирования данных из одного матричного регистра в другой (тоже матричный) предназначена функция:
Можно скопировать строку с номером index из матричного регистра src в каждую строку возвращаемого матричного регистра:
Можно инициализировать каждый элемент матричного регистра одним и тем же скаляром:
Если указать индекс элемента матричного регистра, то можно скопировать скаляр только в этот элемент, не изменяя другие:
И наоборот, можно вернуть как скаляр значение элемента матричного регистра с указанным индексом:
Перечисленным интринсикам копирования соответствуют следующие инструкции:
Вспомогательные операции
Нам осталось рассмотреть небольшую группу вспомогательных операций.
Первая — для того, чтобы обнулить все элементы матричного регистра:
Ему соответствует следующая инструкция:
Фактически это частный случай рассмотренного в предыдущем подразделе интринсика копирования скаляра в каждый элемент матричного регистра, если в качестве скаляра передавать в него ноль:
Вторая — возвращение всего матричного пространства в исходное состояние:
На ассемблере это выполняется следующим образом:
Небольшой пример
Реализуем при помощи матричного расширения от T-Head простейший пример — поэлементное произведение блоков матриц.
Начинаем мы с подключения соответствующего заголовочного файла:
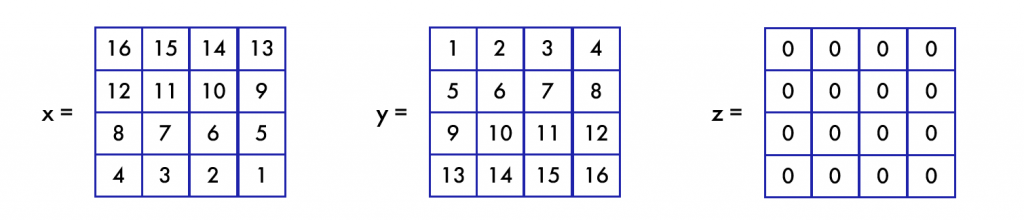
Как уже было сказано, поэлементные операции определены только для целочисленных матриц. Инициализируем 3 матрицы 4\times4 с элементами одинарной точности:
В традиционном двумерном представлении заданные матрицы имеют следующий вид:
Поскольку мы хотим выполнять умножение не для полных матриц, а только для отдельных блоков, сразу рассчитаем stride. Он необходим для корректной загрузки блока в матричный регистр и выгрузки из него:
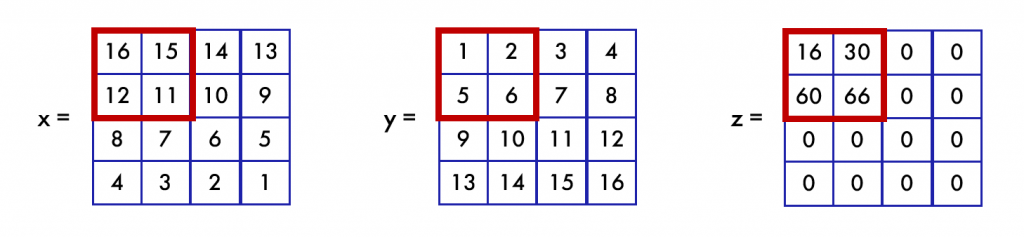
Дальше необходимо загрузить в матричные регистры те блоки, над которыми мы собираемся производить операцию. Пусть для примера мы хотим перемножить только блоки размера 2 \times 2, выделенные на рисунке:
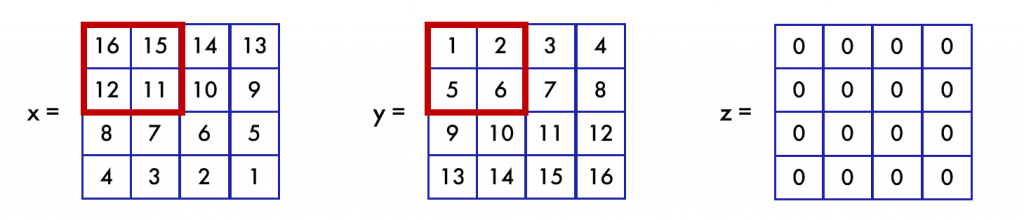
Задаем размер блока:
Вспоминаем, что третья размерность у нас будет конфигурироваться как число элементов в строке, умноженное на их ширину:
Теперь у нас есть все для того, чтобы сконфигурировать матричные регистры для поставленной задачи:
Теперь мы можем загрузить блоки-сомножители в матричные регистры, не забывая указывать stride:
После этого мы производим операцию поэлементного умножения над этими блоками:
Нам осталось только лишь выгрузить результат из матричного регистра ans в соответствующий блок матрицы z. Здесь, опять же, необходимо помнить, что мы работаем не со всей матрицей, а только лишь с блоком внутри нее. Поэтому необходимо указывать stride для выгрузки, чтобы элементы из матричного регистра попали на корректные позиции внутри матрицы:
В итоге получаем следующий результат:
Сохраним представленный выше код в файл pointwise_matmul.c. Его можно скомпилировать и запустить с помощью тулчейна и эмулятора из репозитория. При компиляции важно указывать архитектуру, поддерживающую данное матричное расширение:
При запуске на эмуляторе также необходимо указывать соответствующую архитектуру и флаг матричного расширения:
Заключение
В этом тексте мы познакомились с независимым матричным расширением RISC-V от компании T-Head. Разобрали его спецификацию, особенности конфигурирования матричных регистров и простейший пример использования данного расширения для поэлементного умножения матриц. Пример можно скомпилировать и запустить с помощью тулчейна и эмулятора из репозитория.
Теперь вы полностью готовы к тому, чтобы реализовать при помощи T-Head RVM один из наиболее критичных для производительности многих приложений алгоритмов — умножение плотных матриц. Основные идеи для высокопроизводительной реализации этого алгоритма мы рассмотрели в первом тексте нашего «цикла» про матричные расширения.
В следующем тексте мой коллега, Андрей Соколов, подробно объяснит, как применять эти идеи на практике, а также покажет, как использовать T-Head RVM для низкоуровневой оптимизации матричного умножения.