
Знакомство с цифровыми сигналами
Для передачи информации в электронике используются цифровые сигналы. В этой статье мы с вами разберемся, что это такое и почему компьютеры используют только цифры 0 и 1. А еще научимся переводить привычные десятичные числа в двоичные и проведем несложный эксперимент, который позволит увидеть цифровой сигнал на макетной плате без специальных измерительных приборов.
- что такое цифровой сигнал, бит и байт
- почему компьютеры используют двоичную систему счисления
- как перевести десятичное число в двоичное
- как увидеть цифровые сигналы на макетной плате
Аналоговый и дискретный сигнал
В предыдущем материале вы познакомились с аналоговыми сигналами, хотя это понятие явно не упоминалось. Вы использовали их, когда крутили ручку переменного резистора, чтобы управлять яркостью светодиода. По определению это меняющиеся во времени электрические величины (токи или напряжения), значения которых аналогичны породившему их физическому процессу или порождаемому ими процессу.
Увеличивая электрический сигнал — напряжение между затвором и истоком транзистора, вы увеличивали и яркость светодиода. Зависимость яркости от напряжения была нелинейной, поскольку нелинейна и ВАХ транзистора. Но она была однозначной: дали больше напряжение — светодиод вспыхнул ярче, и наоборот. В этом эксперименте вы видели, как электрический сигнал порождал физическое явление.
Обратная ситуация, когда физическое явление порождает электрический сигнал, справедлива для электронного датчика температуры — термопары. Это устройство, которое состоит из двух сваренных друг с другом разных металлов. Инженеры экспериментально подобрали их таким образом, что при разнице температур в точке сварки металлов и их свободных концов между свободными концами термопары возникает напряжение. Оно зависит от разности температур: нагрели стык термопары — напряжение на концах стало больше, охладили — меньше. Получается, электрический сигнал, в нашем случае напряжение, аналогичен породившей его физической величине — температуре.

Другим хорошо вам известным примером преобразования физических явлений в электрические сигналы и обратно будет работа со звуком. Микрофон улавливает звуковые волны и преобразует их в напряжение, величина которого зависит от громкости и высоты голоса. Потом это напряжение изменяется нужным образом внутри электронной схемы, например, усиливается и подается на динамик, который преобразует его в звук, но уже с другими характеристиками.
Из этих примеров мы видим, что электрический сигнал сам по себе мало интересен, его обычно нужно во что-то преобразовать. В свое время инженеры-схемотехники создали огромное количество разнообразных схем, которые умеют выполнять практически любые математические действия над аналоговыми электрическими сигналами. Это не только сложение и умножение, но и замысловатые операции интегрирования и дифференцирования, которые изучают в курсе высшей математики в университетах. На подобных схемах успешно работали аналоговые компьютеры.
Аналоговые вычислители хорошо работают для конкретной задачи, под которую их разрабатывали. Самым древним представителем аналоговых компьютеров считается так называемый Антикитерский механизм, который автору довелось наблюдать в Афинском археологическом музее. В этом уникальном изделии с помощью шестеренок, эксцентриков и других чисто механических элементов выполнялось вычисление положения Луны и наблюдаемых планет Солнечной системы с довольно высокой точностью!
Электронные аналоговые компьютеры использовались, например, для решения систем уравнений или моделирования перемещения элементарных частиц. Но в любом случае для иной задачи нужно конструировать новый аналоговый вычислитель — очень неудобно.

Вот если преобразовать аналоговый сигнал в поток чисел, соответствующих его величине через определенные интервалы времени, и работать дальше с этими числами — вот это гораздо приятнее! Числами, в отличие от аналоговых сигналов, можно манипулировать как угодно. Самое ценное, что их можно запоминать в электронных схемах и потом производить операции над этими числами в произвольном порядке. Аналоговые сигналы тоже раньше умели записывать, но памятью для них служила намагниченная лента или даже кинопленка, а это очень сильно усложняет электронную систему.
Как же оцифровать аналоговый сигнал? На рисунке ниже показано, как мы можем запрашивать, допустим, через одинаковый интервал времени T отсчеты напряжения с термопары, установленной в уличном термометре. Преобразование этих милливольт в числа выполняют электронные аналого-цифровые преобразователи (АЦП).

Подобные отсчеты производятся не непрерывно, а через определенные интервалы. Хотя бы потому, что на преобразования напряжения в число требуется время. Или, как в случае с уличным термометром, потому что нам не требуется слишком часто снимать его показания. Считать эти данные аналоговыми сигналами уже нельзя. Такие сигналы называют дискретными, то есть прерывистыми.
С какой периодичностью нужно брать эти отсчеты непрерывного сигнала, чтобы не исказить информацию в нем, определяет теорема Котельникова. Но это строгое доказательство проходят в технических вузах уже после освоения высшей математики. Поэтому сейчас просто поверьте на слово: преобразование аналоговых сигналов в числа без потерь информации возможно.
Десятичная и двоичная системы счисления
Итак, мы получаем поток дискретных чисел, которые описывают изменения параметров сигнала во времени. А что это за числа-то? Мы, люди, используем десятичные, потому что у нас 10 пальцев, с помощью которых мы учились считать в раннем детстве. У компьютера пальцев нет, как тогда он считает? Давайте разбираться.
Наша система счисления полностью называется позиционной десятичной. У нее довольно сложное определение: такая система формируется за счет умножения стоящей в определенной позиции цифры на число 10 в степени, задаваемой позицией цифры в числе. Разберем на понятном примере, что это значит. Возьмем число 325. Самая правая цифра в нем означает количество единиц, вторая справа — десятков, третья — сотен. Иначе говоря:
Или если воспользоваться степенями десяти (вспомним при этом, что в математике нулевая степень числа равна 1):
Мы не можем при записи числа перепутать позиции десятков и сотен, потому что получится другое число — 235. Позиция должна однозначно определять, на что мы умножаем записанную в ней цифру. Вот откуда берется такое название привычной нам системы счисления.
Цифровой сигнал
Теперь вернемся к электронике. Там нельзя писать цифры на листочке карандашом, все можно передавать и обрабатывать только с помощью токов или напряжений. Минимальное напряжение в схеме, отсчитываемое от минуса питания, равно 0 В, а максимальное — напряжению на плюсе питания. Мы могли бы разбить весь этот интервал на 10 одинаковых частей и таким образом закодировать 10 цифр разными напряжениями. Такую электронную систему можно создать, и теоретически она будет успешно работать.
Однако на практике не бывает ничего идеального. Из-за разнообразных внешних воздействий и факторов окружающей среды, например, температуры, снижения напряжения питания или помех, уровни сигналов внутри электронной схемы могут «уплывать» от заданных значений. В современных микропроцессорах напряжения питания вычислительных ядер уже имеют значение менее 1 В! Если мы будем разбивать такой небольшой диапазон на 10 частей, то даже при небольшой помехе может легко быть передана цифра 5 вместо 7. Инженеры говорят в таких случаях, что у подобной системы низкая помехоустойчивость.
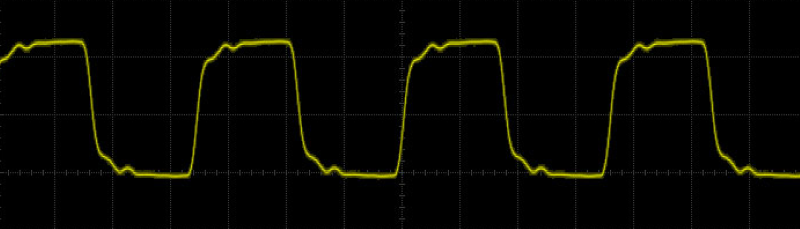
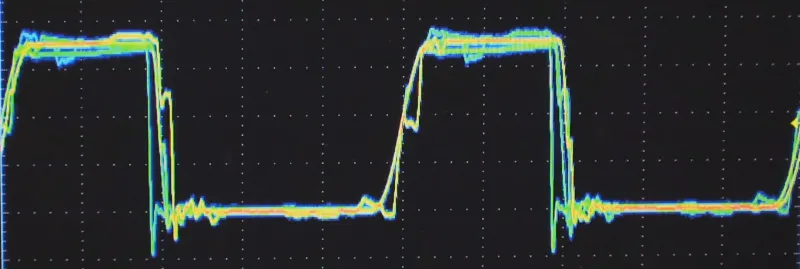
Теперь разделим весь доступный диапазон напряжений на две части: все, что ниже половины напряжения питания, будем считать нулем, а выше — единицей. Помехоустойчивость такой системы будет максимально возможной. Надежность превыше всего! Именно поэтому в цифровой электронике издавна используется позиционная двоичная система, которую изучают на уроках информатики в школе. Решения диктует физика работы реальных, а не теоретических систем.
В этом месте надо сделать важное примечание. Если смотреть документацию на цифровые микросхемы, к которым мы перейдем в дальнейшем, то окажется, что в реальных системах диапазон напряжений разбивается на три части! При этом система остается двоичной, а не троичной. В некоторой полосе напряжений вблизи половины питания у нас находится неопределенное состояние, когда нельзя сказать, ноль или единица сейчас в данной точке системы. Например, для тех устройств, которые мы будем проектировать на макетной плате с питанием 9 В, мы будем считать, что логический ноль находится в диапазоне напряжений от 0 В до примерно 3 В. А логическая единица — от приблизительно 6 В до 9 В. От 3 В до 6 В — значение числа не определено.
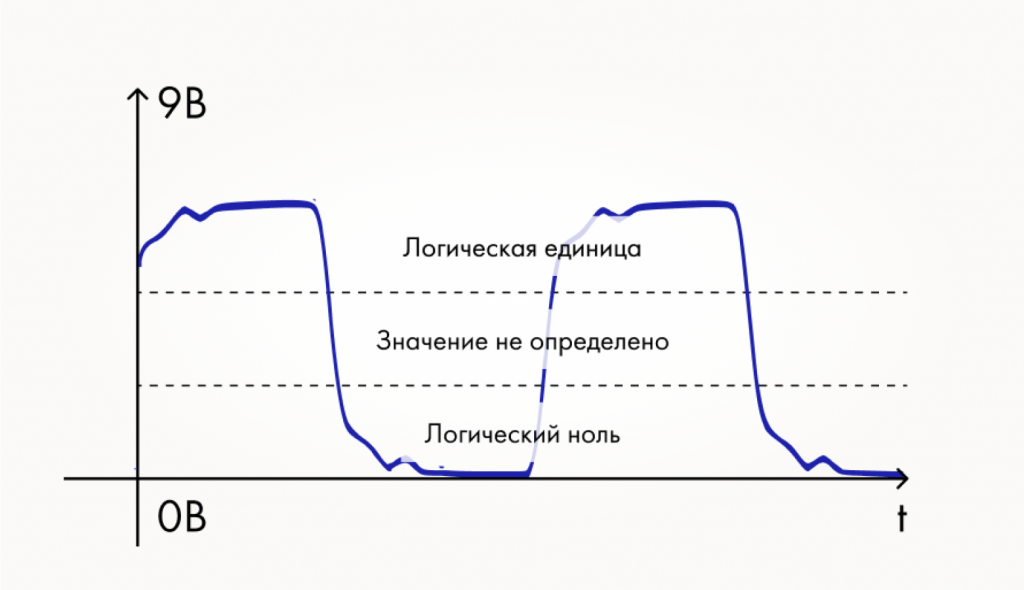
Наверняка, вы подумали: «Только мне стало все понятно, как автор опять вносит сумятицу. Зачем еще эта третья область?!» Дело в том, что, опять же, мы работаем с реальными, а не идеальными полупроводниковыми приборами. И их параметры могут «гулять» в определенных пределах. Если на вход конкретной цифровой схемы подать сигнал, находящийся вблизи половины питания, то предсказать, сочтет она его логическим нулем или единицей, невозможно. Поэтому лучше вообще избегать этого диапазона напряжений.
К счастью, цифровые сигналы переключаются между высоким и низким уровнями настолько быстро, что проскакивают эту область неопределенности без сбоев в интерпретации. А к отклонениям от идеала внутри разрешенных коридоров напряжений логического нуля и единицы цифровые схемы относятся спокойно. Непросто все в реальном мире, где нолики и единички — не просто цифры на бумаге или в программном коде, не так ли?
Итак, в наших устройствах мы используем всего две цифры: ноль и единицу. Двоичное число 101 раскладывается на слагаемые и множители, но уже по основанию 2, а не 10:
Двоичные числа намного длиннее десятичных. Поэтому в цифровой вычислительной системе нужно передавать гораздо более длинные последовательности цифр. Но, что поделать, помехоустойчивость требует таких жертв.
Перевод из десятичной системы в двоичную
Посмотрим на общий принцип перевода из десятичной системы в двоичную по шагам.
Шаг 1. Находим максимально близкую к десятичному числу степень двойки, которая будет меньше либо равна исходному десятичному числу.
Возьмем число 10. Ближайшая степень двойки — это 8, два в кубе.
Шаг 2. Все десятичные числа кроме 0 начинаются с единицы в какой-то позиции. Так что теперь нам нужно понять, в какую позицию мы напишем свою первую единицу.
Нужно посмотреть на степень двойки. Первая позиция — самая правая. Она соответствует двойке в нулевой степени, вторая позиция — двойке в первой степени, третья позиция — двойке в квадрате, ну, а наш куб — это третья степень, то есть четвертая позиция справа.
Записываем единицу в четвертый разряд двоичного числа: 1???
Шаг 3. Теперь нам нужно понять, что писать в следующую — третью позицию. Для этого находим остаток от нашего исходного десятичного числа. Это будет двойка (10 − 8). Такой остаток не делится на два в квадрате (2/4), которое соответствует третьей позиции.
В третьей позиции пишем ноль: 10?
Шаг 4. Повторяем операцию для разности исходного числа и найденной степени двойки до тех пор, пока не дойдем до последнего разряда. Наш остаток — двойка, равен двойке в первой степени, поэтому во второй позиции в двоичной записи появляется единица.
101?
Шаг 5. Остаток (2 − 2) равен нулю. Значит в первой справа позиции появляется ноль.
Итого, 10 в двоичной системе — это 1010.
Перевод из двоичной системы в десятичную проще: умножаем единицы в записи числа на соответствующие им степени двойки и складываем все произведения. Например, наше число 1010:
Программисты и разработчики цифровой электроники без запинки назовут первые степени двойки от нулевой до десятой, потому что эти числа постоянно используются в работе: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024. Полезно их выучить для быстрого пересчета из двоичной системы в десятичную и обратно.
Более простой по применению вариант перевода из десятичной системы в двоичную таков. Исходное десятичное число делим на 2. Какой получится остаток от деления — 0 или 1 — то число и записываем в первый (самый правый) разряд двоичного числа. Затем частное снова делим на 2 и остаток записываем во второй разряд. И так продолжаем до тех пор, пока очередное частное не станет равным 0. Переведем десятичное число 9 в двоичное этим способом:
- 9: 2 = 4 с остатком 1, в нулевом разряде пишем 1;
- 4: 2 = 2 с остатком 0, в первом разряде пишем 0;
- 2: 2 = 1 с остатком 0, во втором разряде пишем 0;
- 1: 2 = 0 с остатком 1, в третьем разряде пишем 1.
Результат преобразования в двоичной системе будет таким: 1001.
Поскольку самый правый разряд числа имеет самое маленькое значение по величине, то его называют младшим значащим разрядом, сокращенно МЗР. Еще про него говорят, что он имеет наименьший вес в числе. А самый левый разряд «весит» больше остальных, поэтому он именуется старшим значащим разрядом, или СЗР. То есть в двоичном числе 1010 младший значащий разряд равен нулю, а старший значащий разряд — единице. А в десятичном числе 456 МЗР равен 6, а СЗР — 4.
Каждый разряд двоичного числа называется битом. Число, содержащее в себе восемь битов, называется байтом. Одним байтом можно закодировать числа от 0 до 255. Применяется и байтовая запись — в ней число 5 выглядит как 00000101, а 15 представляется как 00001111. Нули в старших неиспользуемых разрядах не отбрасываются, чтобы все числа были одинаковой длины для удобства восприятия. Если нужны еще большие значения, то используют несколько байтов, зачастую отделяя их на письме друг от друга пробелами, чтобы не запутаться в длинном потоке нулей и единиц.
Программисты и разработчики электроники любят еще использовать шестнадцатеричную и восьмеричную системы счисления. В первой используются 10 цифр из привычной нам десятичной системы для обозначение тех же чисел от 0 до 9, а остальные шесть чисел обозначаются буквами: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15. Во второй же используются только первые 8 цифр, от 0 до 7.
Физического воплощения эти две системы счисления не имеют, а используются лишь для того, чтобы заменить длинные двоичные числа более компактными вариантами записи. Так, вместо двоичного 11111001, равного десятичному 249, в шестнадцатеричной системе нужно написать всего два символа: F9, а в восьмеричной — 371. Намного компактнее, чем поток двоичных битов. Использовать эти две системы в наших материалах мы не будем, поэтому более подробное их описание и примеры применения вы можете найти в других источниках, если потребуется.
Решите несколько задач без калькулятора — в уме или на бумаге:
1. Переведите десятичные числа 31, 47, 12, 122, 207 в двоичные любым удобным вам способом.
2. Переведите двоичные числа 111, 1011, 10101, 110011, 1001110 в десятичные.
3. Решите неравенства, в которых слева — двоичное число, а справа — десятичное: 11110? 22, 1001? 11, 100110? 50, 10101? 19. Пример ответа: 110011 > 41.
Ответы даны в конце статьи.
Двоичная система на макетной плате
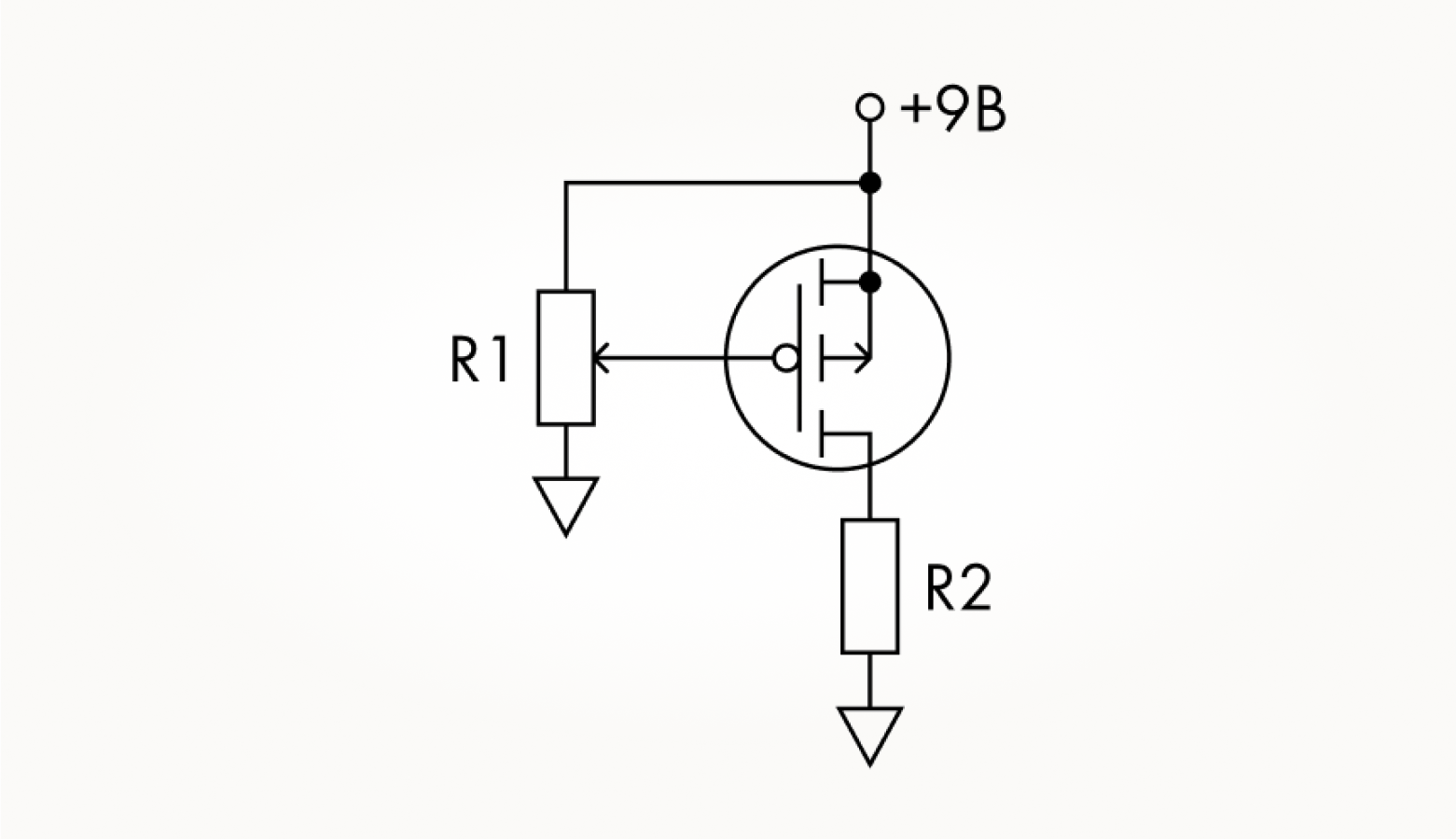
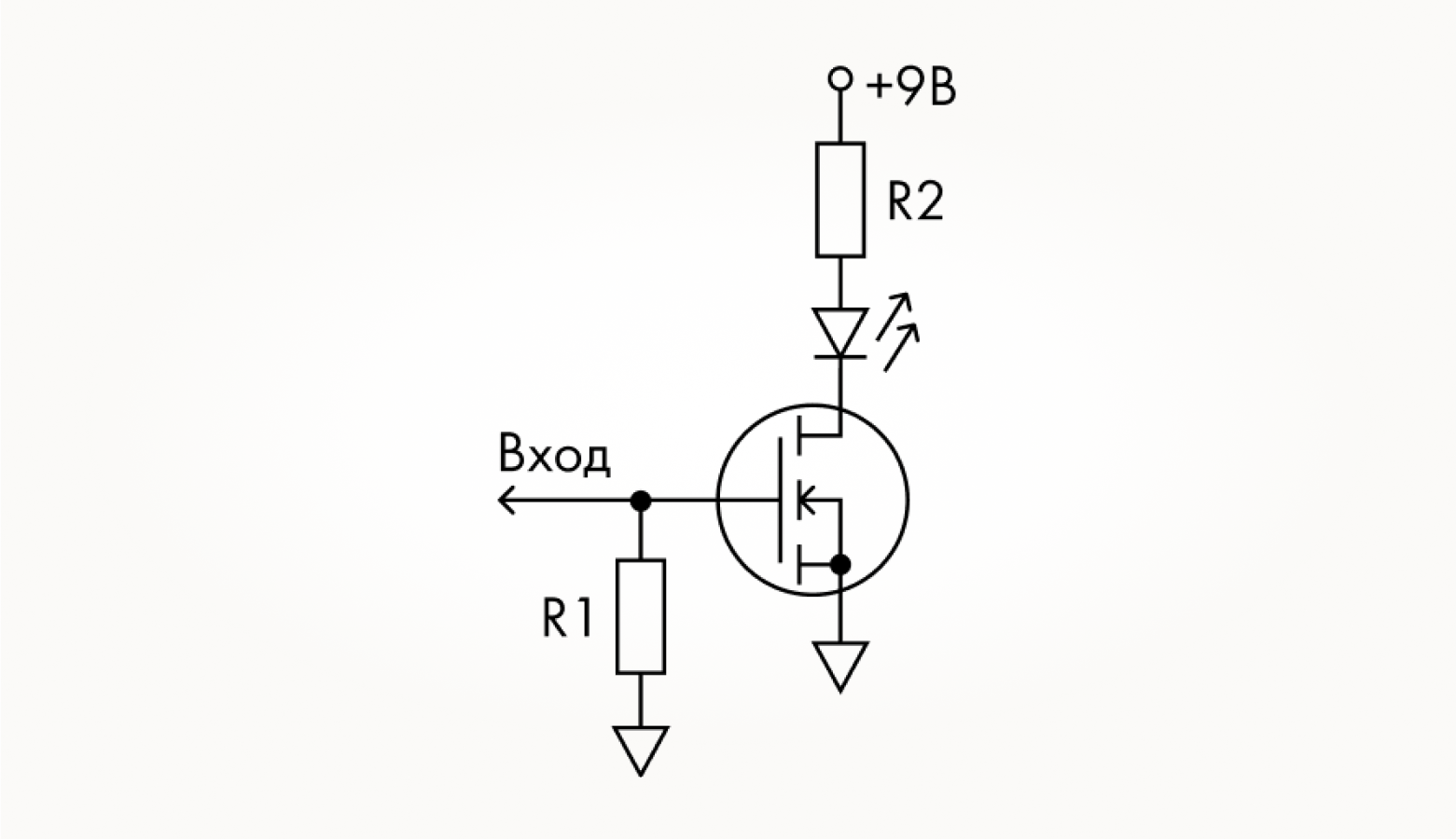
Хватит уже теории, настало время переходить к практике! Для начала давайте разберем задачу на разработку схемы регулятора яркости светодиода на p-канальном транзисторе и схемы для измерения ВАХ. Выглядеть они должны вот так:
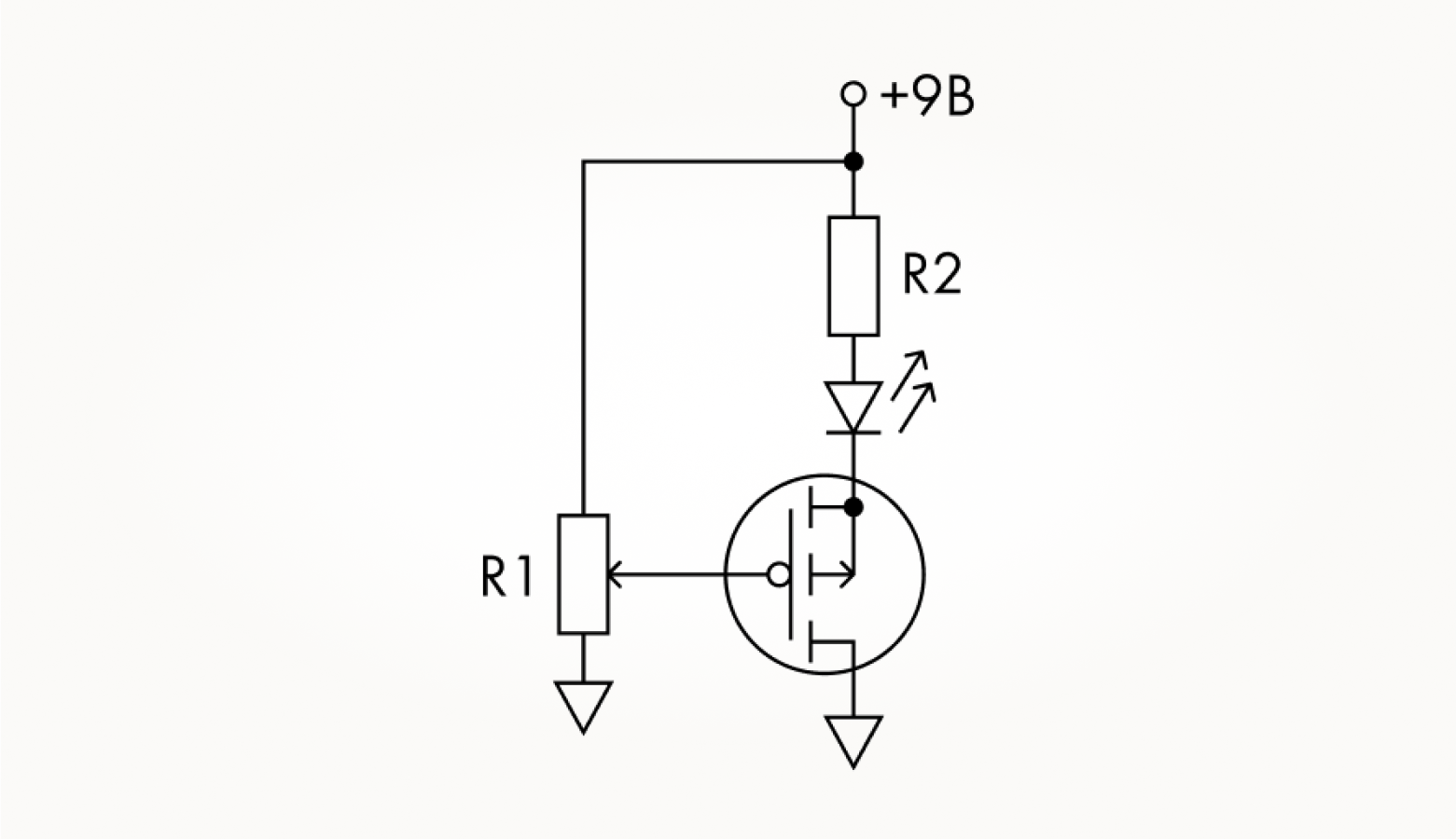
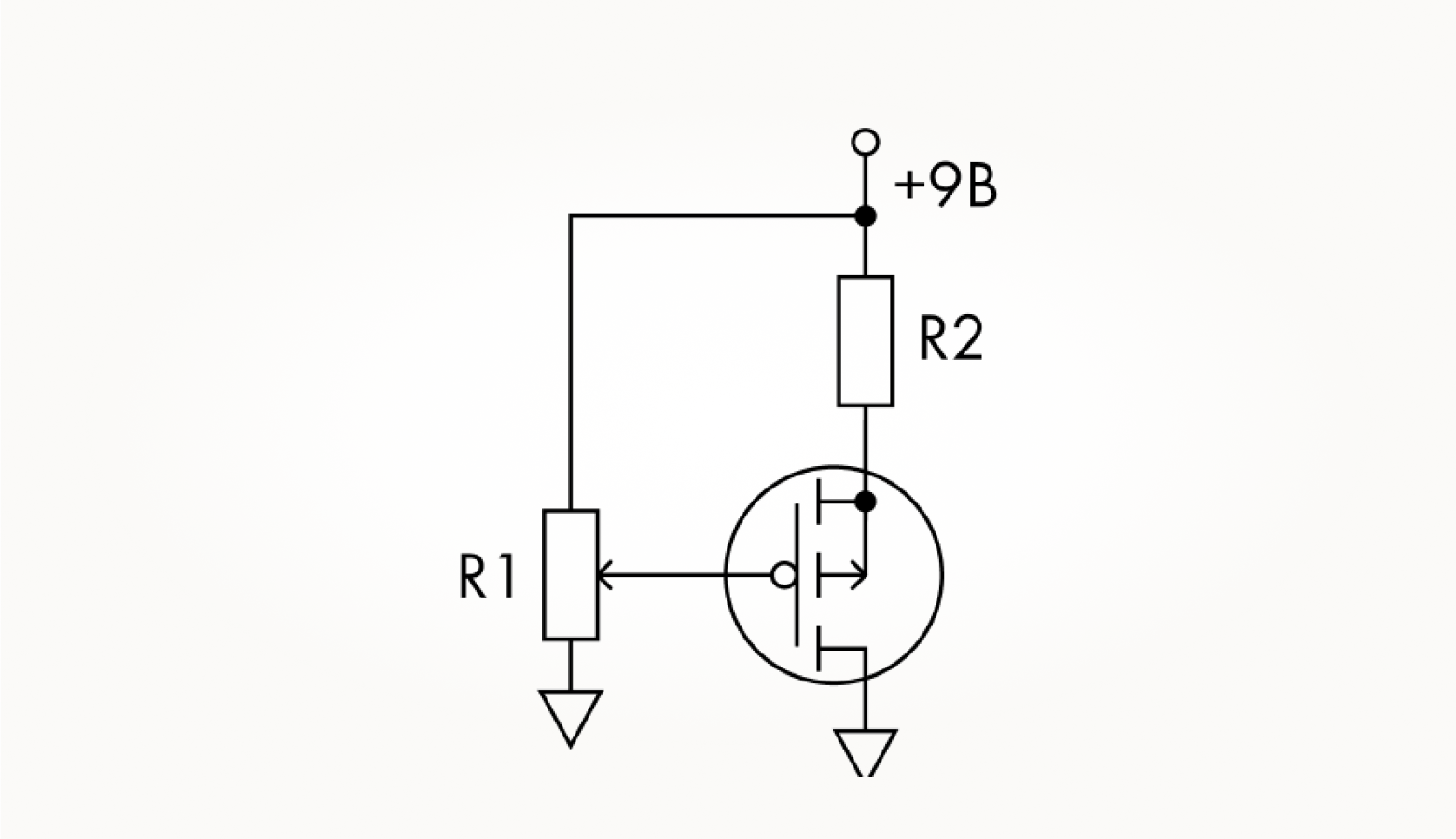
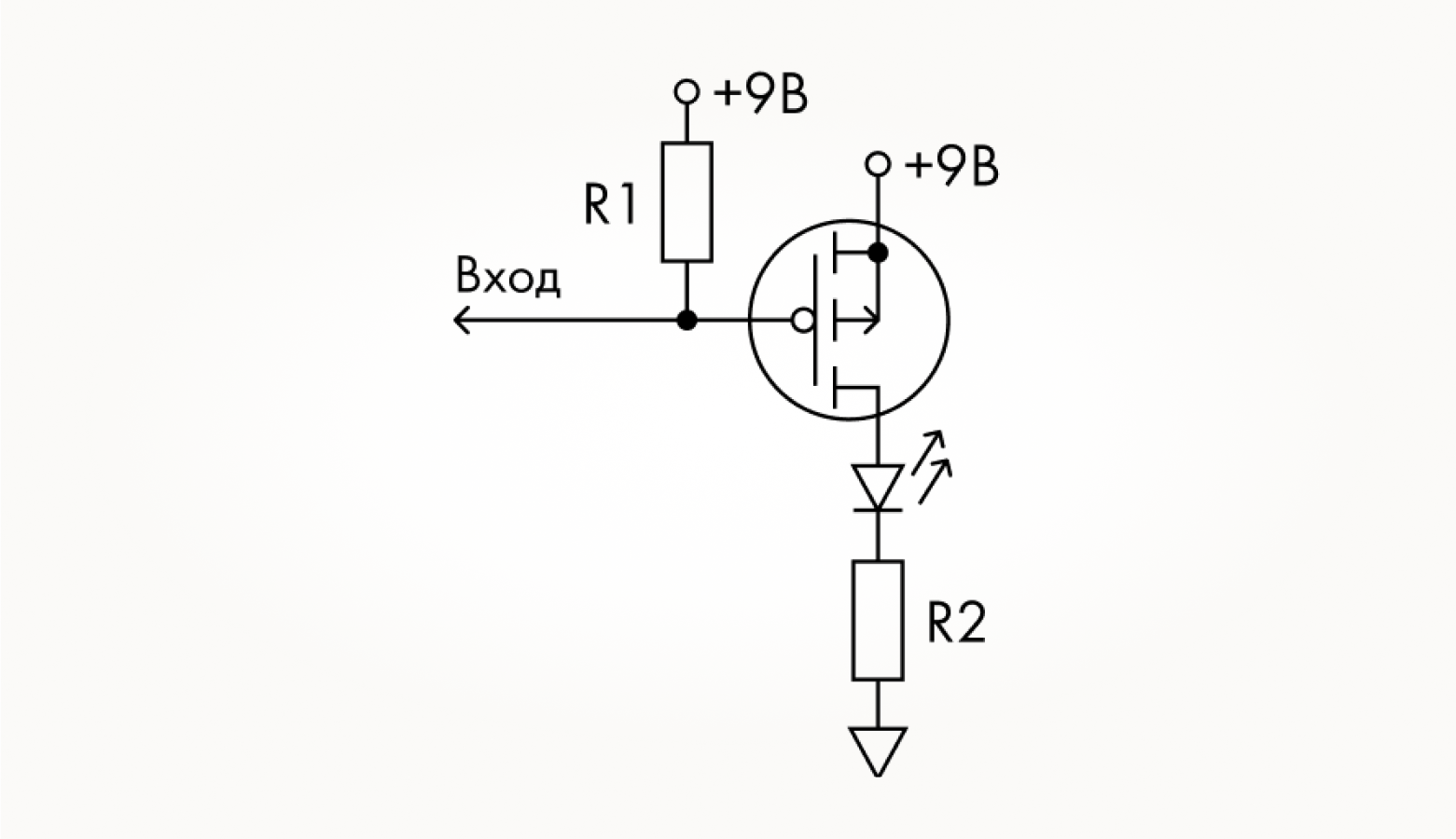
Иногда их пытаются реализовать вот так:
Эти варианты в нашем случае неправильные. Почему это так, хотя, на первый взгляд, схема рабочая и на макетной плате все функционирует неплохо, будем разбирать в ролике с мультиметром в руках. Неправильность здесь условная, только для наших задач, поэтому в подписях к рисункам она взята в кавычках. Существует целый пласт аналоговых схем, в которых полезная нагрузка (в нашем случае это светодиод с резистором) подключается в цепь истока. Но в цифровой электронике, построенной на МОП-транзисторах так не делается по причинам, которые будут очевидными после просмотра ролика.
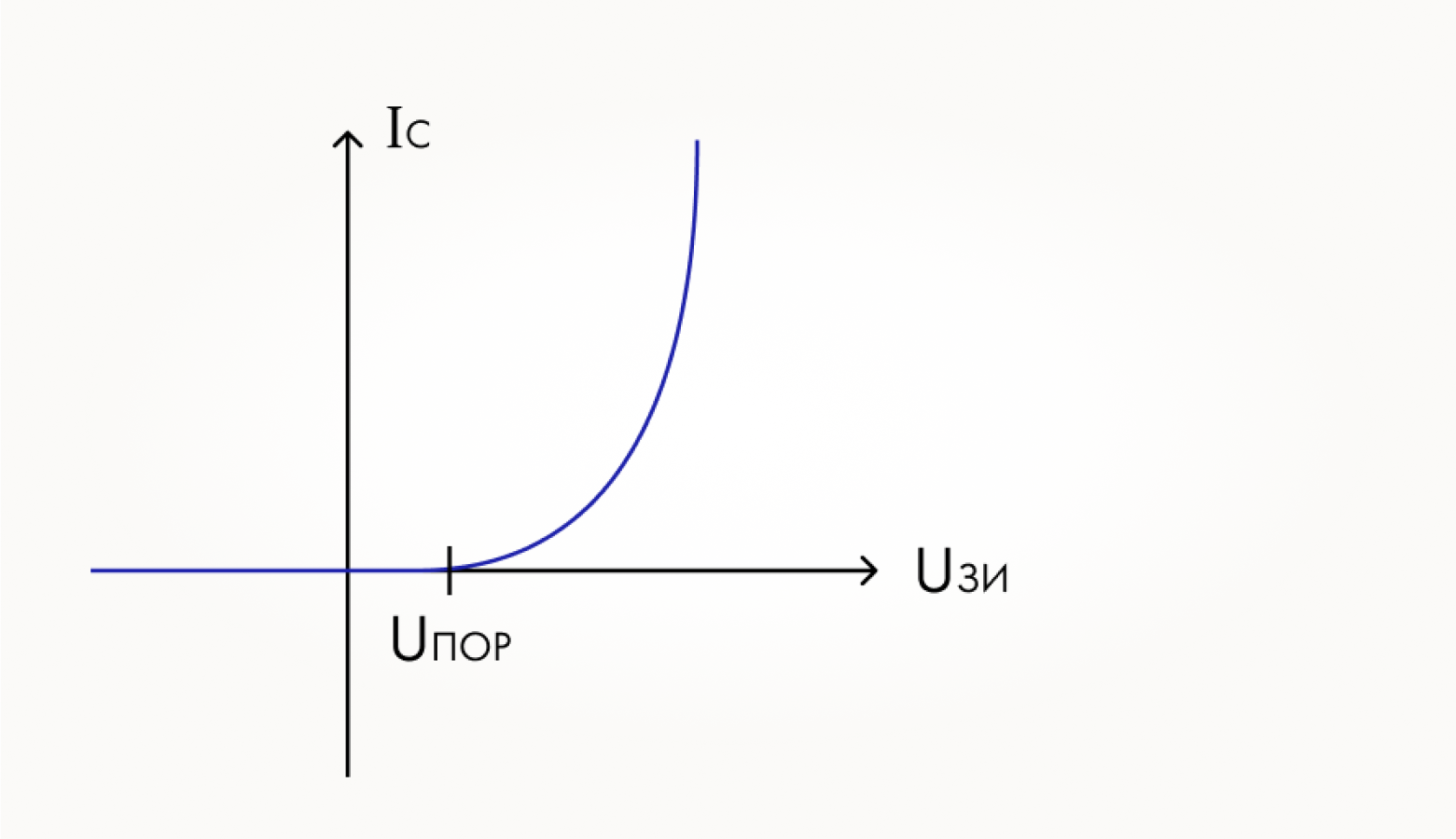
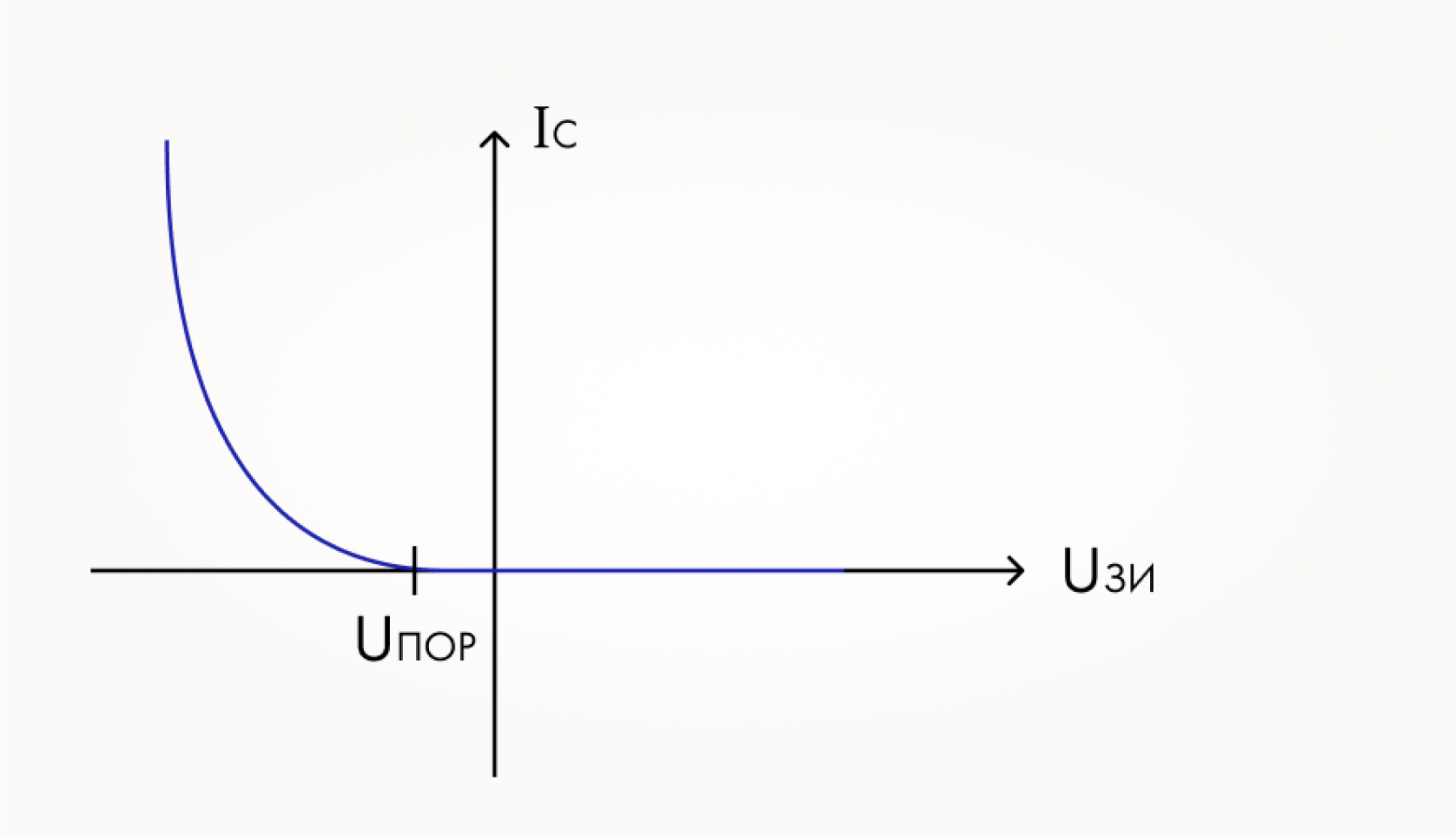
Но на деле не так уж важно, какой вариант схемы был выбран. Даже при неправильном включении p-канального транзистора видно, что ток через него течет тем больше, чем ближе к нулю напряжение на затворе. А у n-канального все точно наоборот: ВАХ каждого из приборов выглядит, как показано на рисунке (напомним, что по горизонтальной оси откладывается напряжение между затвором и истоком, а по вертикальной — ток стока):
Как же так вышло, что ВАХ p-канального транзистора лежит в области отрицательных напряжений? Это как раз вопрос договоренностей, что считать точкой отсчета разности потенциалов, про который шла речь во второй главе. Дело в том, что если мы рассматриваем отдельный транзистор, не включенный в схему, то на графике ВАХ мы по горизонтальной оси откладываем напряжение затвор-исток. То есть из напряжения на затворе мы вычитаем напряжение истока. Исток n-канального прибора в цифровых схемах направлен в сторону минуса питания, а то и прямо подключен к нему. И на затвор нужно подать напряжение больше, чем напряжение на истоке, чтобы в транзисторе образовался проводящий электронный канал, и через него потек ток.
А p-канальный транзистор устроен прямо противоположным образом. Поэтому его исток направлен в сторону плюса питания, а на затвор для образования дырочного проводящего канала должно подаваться напряжение меньше, чем напряжение истока. Отсюда и получается чисто математически, что если мы вычтем из напряжения на затворе напряжение на истоке, то в этом случае получим отрицательную величину. И график ВАХ примет тот вид, что на рисунке выше. Поэтому в документации на n-канальный транзистор может быть указано, что его пороговое напряжение равно, допустим, 3 В, а на p-канальный: −3 В.
Если же мы рассматриваем транзисторы, включенные в какую-то схему, то, как условились раньше, за ноль — начало отсчета напряжений — мы принимаем минус батарейки питания. И получается, что в данной системе отсчета с питанием, например, 9 В упомянутый в предыдущем абзаце n-канальный транзистор включается при напряжении около 3 вольт, а p-канальный — при напряжении ниже 6 вольт. Никаких отрицательных значений уже нет. Эта некоторая путаница раздражает даже начинающих инженеров: то отрицательные вольты, то они положительные. Но, что поделать, так сложилось исторически. В ролике это все разобрано и показано подробно.
В дальнейшем нам будет проще, мы будем рассматривать только транзисторы в составе схем, поэтому все напряжения у нас всегда будут строго положительные!
В начале этой статьи описан именно такой общепринятый подход представления двоичных единиц и нулей. То есть мы можем, слегка изменив схемы регуляторов яркости светодиодов, получить схемы индикаторов двоичных нулей и единиц для наших будущих цифровых схем, которые мы собираемся конструировать на макетной плате!
Схемы индикаторов немного отличаются от схем регуляторов. Нам не нужно ничего регулировать, мы хотим только ловить цифровые нули и единицы, поэтому вместо переменного резистора в цепи затвора находится постоянный. Причем он подключен в зависимости от типа транзистора либо к минусу, либо к плюсу питания так, чтобы светодиод в исходном состоянии схемы не горел, то есть транзистор был закрыт. Таким образом, у n-канального затвор через резистор «висит» на логическом нуле или минусе питания, а у p-канального — на логической единице или плюсе.
Вы можете поинтересоваться, а зачем к плюсу или минусу питания подключать затвор через резистор, почему не напрямую? А потому что мы будем еще проводом подключать вход индикатора к интересующей нас точке на макетной плате. Если, например, для n-канального транзистора напряжение в измеряемой точке будет соответствовать логической единице, а изначально его затвор подключен напрямую к логическому нулю, то без резистора возникнет короткое замыкание.
«Хорошо, — скажет пытливый читатель. — Так давайте вообще уберем эту привязку затвора к изначальному уровню, зачем она?»
Дело в том, что, как мы помним из предыдущей статьи, ток не течет через затвор МОП-транзистора, поскольку он отделен от остального транзистора слоем изолятора — оксида кремния. У нас на затворе от предыдущих экспериментов или от того, что мы взялись за его вывод наэлектризованными руками, может быть остаточный заряд, который откроет транзистор даже с никуда не подключенным затвором. И будет у нас не индикатор, а неизвестно что! Поэтому для определенности необходимо задать начальное значение логического уровня на затворе, а для отсутствия короткого замыкания во время работы — сделать это через резистор. Все это показано в ролике с практикой, который вы найдете на полях.
Вот такая примитивная схема позволяет нам увидеть цифровые сигналы на макетной плате без измерительных приборов вообще. Мы часто будем ее использовать и в следующих роликах. Можно доработать ее с помощью тактовой кнопки вместо провода. Нажатие кнопки задает один логический уровень на затворе, а отпускание — другой. Так, быстро нажимая и отпуская кнопку, можно передавать любую последовательность двоичных чисел.
Ответы на вопросы для самопроверки
- 31 = 11111, 47 = 101111, 12 = 1100, 122 = 1111010, 207 = 11001111.
- 111 = 7, 1011 = 11, 10101 = 21, 110011 = 51, 1001110 = 78.
- 11110 > 22, 1001 < 11, 100110 < 50, 10101 > 19.

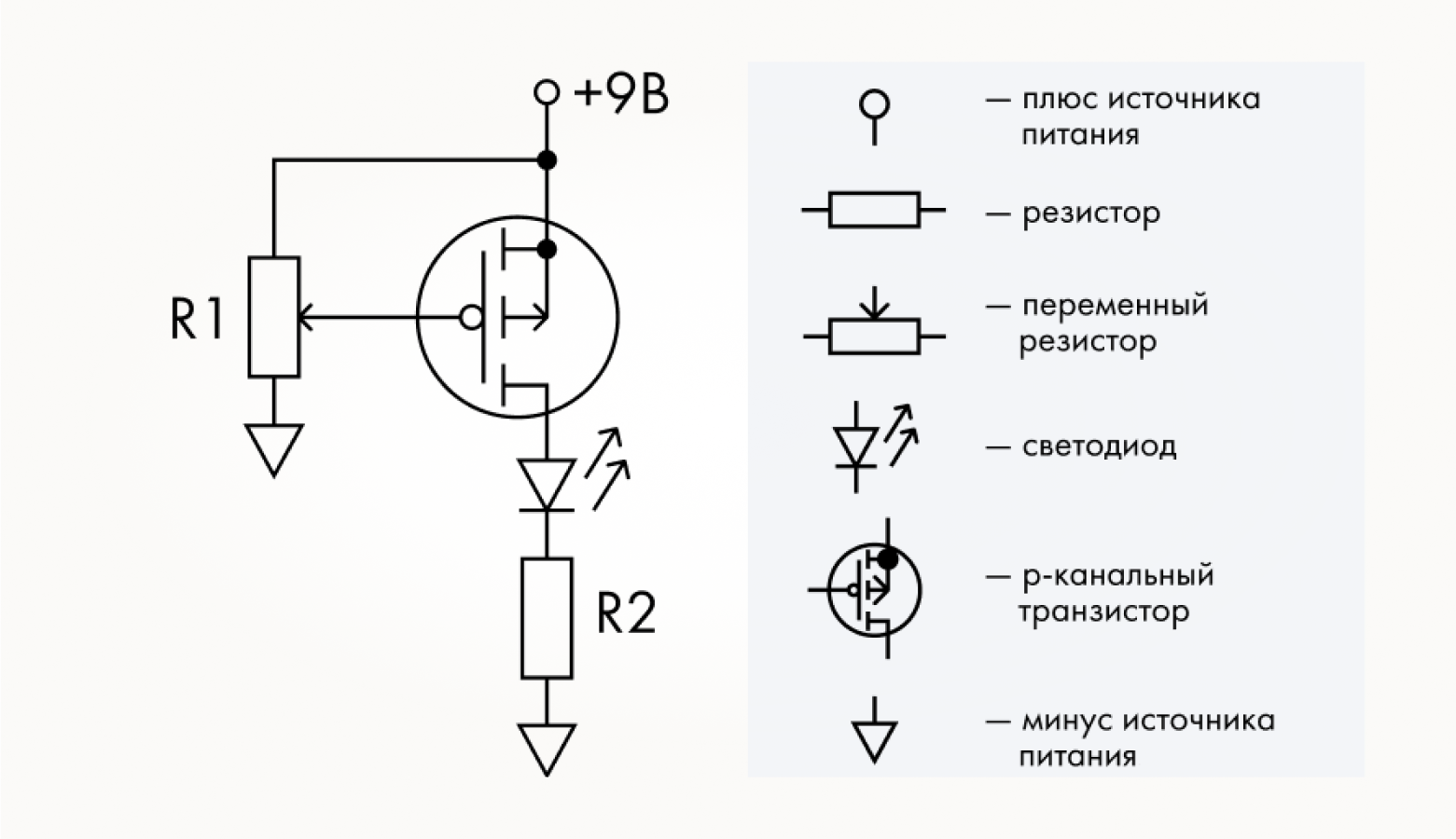
спасибо, очень интересная подача. Единственное, что неудобно — из текста непонятно, какие именно транзисторы используются. Для новичка p-канальный транзистор ни о чем не говорит. По схеме также непонятно сразу, что это МОП.
Я бы предложила указывать список компонентов для каждой конкретной схемы, чтобы не запутаться.
Еще раз спасибо.
Здорово, что вам понравилось! Попробуем помочь разобраться с возникшими вопросами. Список компонентов есть на вводной странице курса — вам нужно скачать файл «Список оборудования для курса по схемотехнике», там мы подробно разбираем, что пригодится. А о транзисторах и принципах их работы наглядно рассказываем в предыдущих главах. Мы задумывали этот материал как часть большого цикла, поэтому изучать материалы лучше последовательно, чтобы ничего не упустить. Ловите ссылку на весь курс: https://engineer.yadro.com/circuits-course
Но вы справедливо заметили, что связь между статьями курса может быть неочевидна. Мы подумаем, как более наглядно представить на странице другие материалы, Спасибо, что подсветили эту сложность)