
Собираем элементы цифровой логики
Электрический ток похож на поток машин в большом городе. Чтобы их движение не превращалось в хаос и они могли предсказуемо приехать из точки, А в точку B, существуют различные регуляторы движения: дорожные знаки, разметка, сфетофоры. Подобные регуляторы есть в схемотехнике, и о них — логических вентилях — мы поговорим в статье.
- какие базовые логические вентили существуют
- как они обозначаются графически
- что такое таблицы истинности и как их составлять
- как создавать цифровые логические схемы на транзисторах по алгоритму
Простая сумма двух транзисторов
В предыдущей статье вы создали на транзисторных ключах два индикатора, реагирующих зажиганием светодиода на разные логические уровни входного сигнала. Давайте попробуем объединить их в одной схеме.
Вы уже знаете, что p-канальный транзистор без потерь передает на выход логическую единицу, а n-канальный прибор — логический ноль. «Без потерь» здесь означает отсылку к нашим экспериментам в предыдущей части, в которых мы подключали нагрузку в цепь истока и наблюдали заметную потерю напряжения на выходе схемы регулятора яркости светодиода в отличие от случаев, когда нагрузка была в цепи стока. Применительно к цифровой электронике, как вы понимаете, такая потеря уровней напряжения снижает помехоустойчивость. Этот полезный опыт нужно обязательно учесть при конструировании цифровых схем на МОП-транзисторах.
Итак, чтобы получить схему универсального индикатора двоичных сигналов, нам нужно сделать следующее:
- объединить их затворы и стоки,
- истоки подключить к плюсу и минусу питания,
- присоединить к выходу такой конструкции два светодиода с ограничивающими ток резисторами.
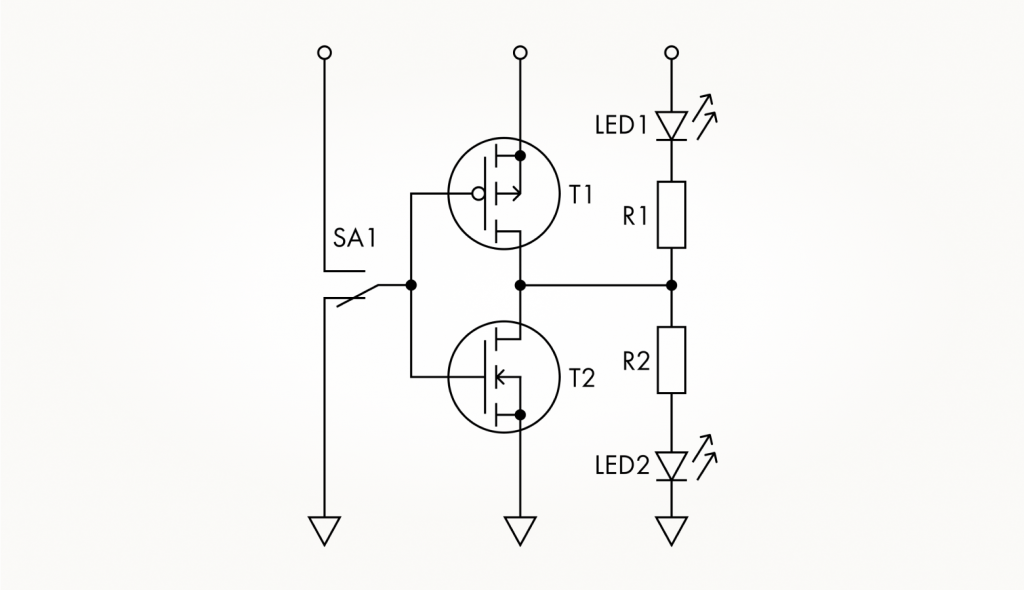
Светодиод LED1 загорится, если на стоках транзисторов логический ноль, а LED2 — при логической единице в этом же узле. Кстати, от подтягивающих резисторов в схеме можно отказаться. Один из светодиодов будет гореть в любом случае, поэтому вообще не важно, в каком состоянии будет переключатель SA1 при подаче питания. Вместо переключателя можно использовать гибкий провод, которым затворы будут присоединяться то к плюсу, то минусы питания вручную.
Давайте проанализируем работу транзисторов в этой схеме.
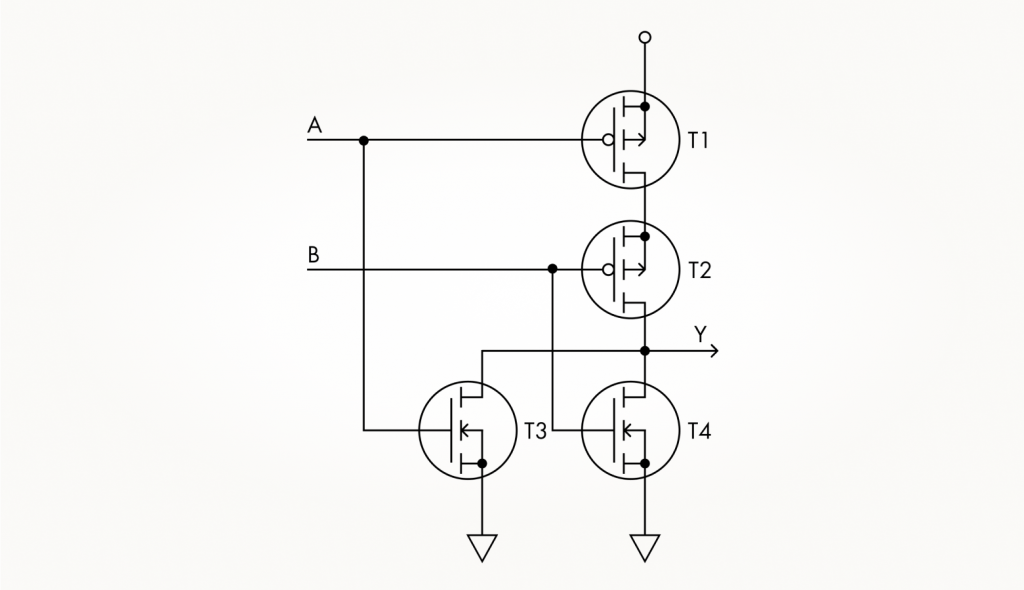
Предположим, что на ее вход, то есть на оба затвора одновременно, подан ноль. Тогда n-канальный ключ T2 будет закрыт, а p-канальный T1 — открыт. И на выход, то есть на оба стока, с плюса питания через T1 будет выдаваться единица без потерь.
Теперь обратная ситуация: на затворы придет единица. Тогда p-канальный транзистор T1 закроется, а n-канальный T2 откроется, и на выходе окажется ноль с минуса питания через T2.
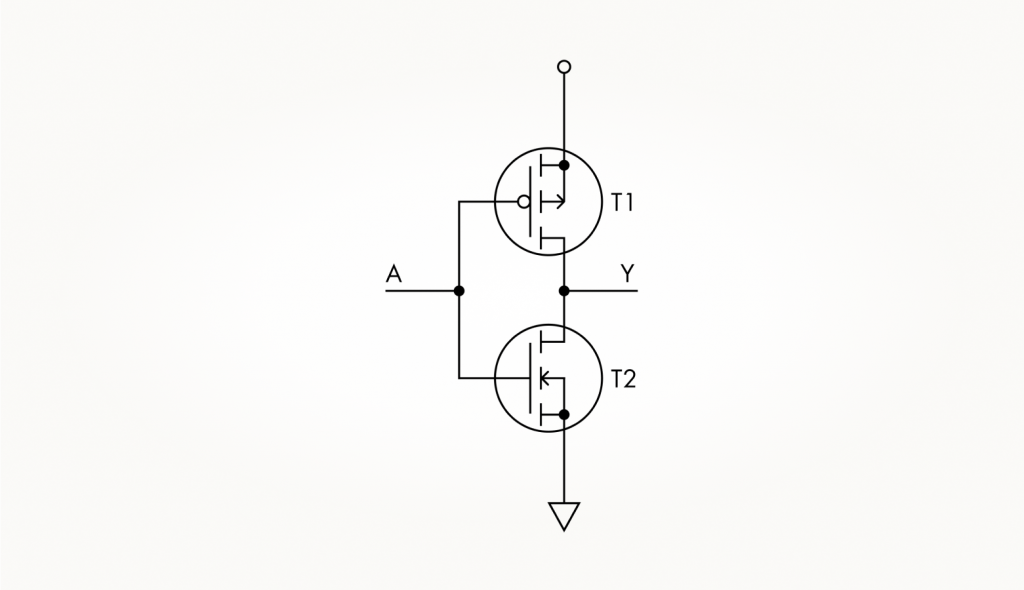
Из двух транзисторов получилось устройство, у которого на выходе сигнал всегда противоположен входному. Это самый простой логический элемент — инвертор (от лат. inversio, переворачивание). На изображении ниже его схема изображена отдельно от остальных, вспомогательных, компонентов: вход инвертора обозначен буквой A, а выход — буквой Y.
Инвертор и другие цифровые элементы, о которых вы узнаете далее, называют вентилями. Тут как вентили в трубопроводе, которые пропускают или перекрывают воду в зависимости от положения рукоятки. Только в электронике вентили логические и управляются не руками, а электрическими цифровыми сигналами. И пропускают они поток двоичных данных вместо воды.
На схемах в отечественной и зарубежной литературе вентили обозначаются по-разному. Чтобы вы не путались в дальнейшем, давайте разбираться.
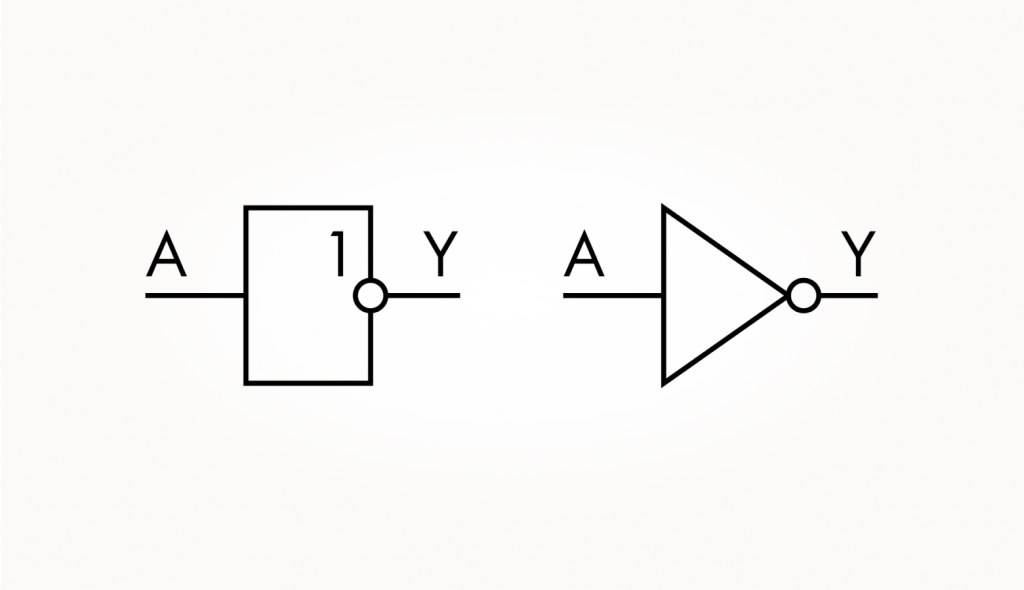
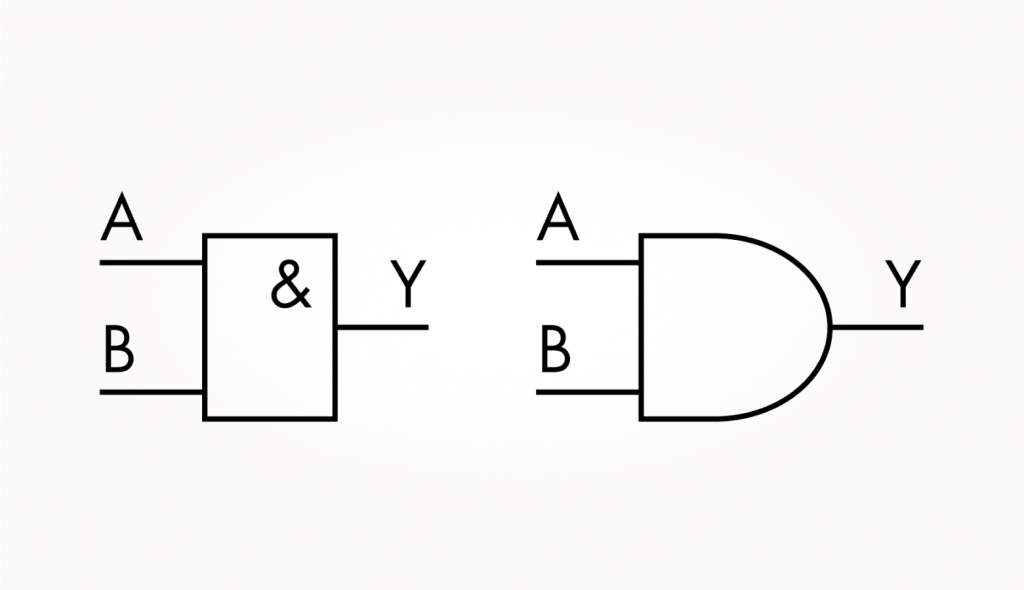
Прямоугольник слева — обозначение инвертора, которое можно встретить в российских источниках, справа — в иностранных. Во всех схемах курса мы используем зарубежные обозначения, у них говорящая форма, которая подсказывает тип вентиля.
В обоих случаях есть общий элемент — кружок возле выхода Y, в электронике он используется для обозначения инверсии. Такой кружок вы могли заметить на использующемся у нас символе p-канального транзистора. Он показывает, что этот транзистор в цифровых схемах открывается логическим нулем на затворе, а не единицей, как n-канальный.
В схеме инвертора есть оба типа транзисторов. Каждый из них хорош в своей работе. Как вы помните, р-канальный обеспечивает на выходе единицу — без потерь по уровню напряжения. Его n-канальный «коллега» так не может, зато он отлично формирует ноль на выходе. Оба транзистора как бы взаимодополняют друг друга.
Если в логических элементах используются оба типа транзисторов, они называются комплементарными МОП-вентилями, сокращенно — КМОП. Слово «комплементарный» как раз означает «взаимодополняющий».
У КМОП-схем есть одно важное достоинство, которое сделало их очень привлекательными для разработчиков. Вернемся к схеме инвертора.
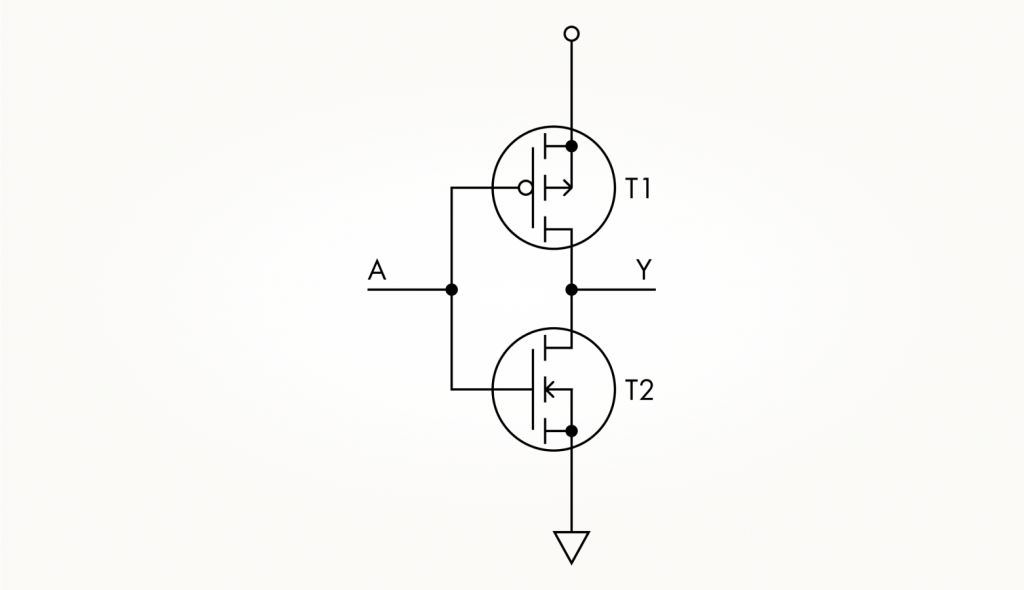
Обратите внимание, что при работе вентиля в любом устойчивом состоянии — нуля или единицы — открыт только один транзистор из двух. Ток в такой схеме между плюсом и минусом питания в стабильном режиме не течет, то есть энергия не расходуется. Сквозной ток через оба транзистора сразу течет только в короткий момент переключения. Таким образом, КМОП-схемы более бережны к энергоресурсам, чем другие типы цифровой логики.
Как можно описать цифровую схему
А теперь давайте составим таблицу. В одну колонку поместим все возможные состояния входа инвертора A, а в другую — состояния выхода Y, которые соответствуют показаниям соседнего столбика.
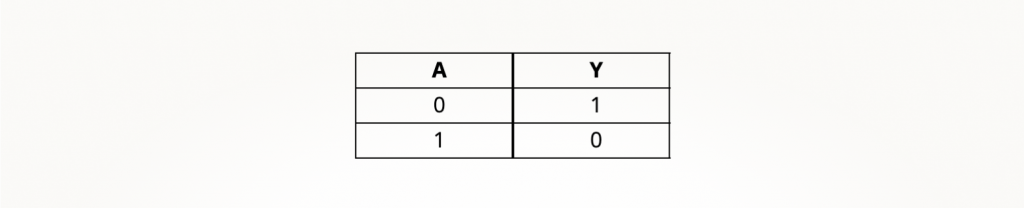
Такая таблица называется таблицей истинности и емко иллюстрирует принципы работы вентиля. Что мы можем понять из таблицы? Что у вентиля есть один вход и один выход, а еще он инвертирует входной сигнал: то есть меняет его на противоположное значение (0 на 1 и наоборот).
Такие таблицы можно составлять и для более сложных вентилей, мы в этом еще потренируется. А можно делать наоборот: по таблице истинности конструировать схему на транзисторах. Такие таблицы — не единственный способ описания цифровых схем, для этого также используют формулы и теоремы из раздела математики, который называется булевой алгеброй, или двоичной логикой.
Какие логические вентили бывают
Мы познакомились с понятием вентиля и его самым простым представителем. Время узнать про другие вентили.
Если вы уже занимались программированием, возможно, вы слышали про логические функции И, ИЛИ, И-НЕ, ИЛИ-НЕ и Исключающее ИЛИ. Если нет, это никак не повлияет на восприятие материала — мы расскажем про них и о про то, как они реализованы на транзисторах.
Логическое И
Представим, что мы разрабатываем микроволновую печь и среди электроники в ней есть два датчика. Один определяет, что мы поставили необходимое время разогревания пищи. Второй, что дверь микроволновки закрыта (и разогретый супчик не запачкает все вокруг). И запустить СВЧ можно только в том случае, если датчики отвечают «ДА». Да — время разогрева выставлено, да — дверь закрыта. Если какое-то из условий не соблюдено (ответ «НЕТ»), супчик будет не разогреть — процесс не запустится.
Цифровая электроника прекрасно подходит для реализации такого алгоритма работы. Ответ «ДА» — это логическая единица, а ответ «НЕТ» — логический ноль. Для конструирования микроволновки нам потребуется цифровой вентиль с двумя входами и одним выходом. И на выходе он должен выдавать единицу только в одном случае: на первый И второй входы пришли единицы. Теперь понятно, почему такой вентиль называется «логическое И», или AND? А вот так он обозначается на схемах (здесь и далее: слева — российское обозначение, а справа — зарубежное).
В таблице истинности логического И строк больше:
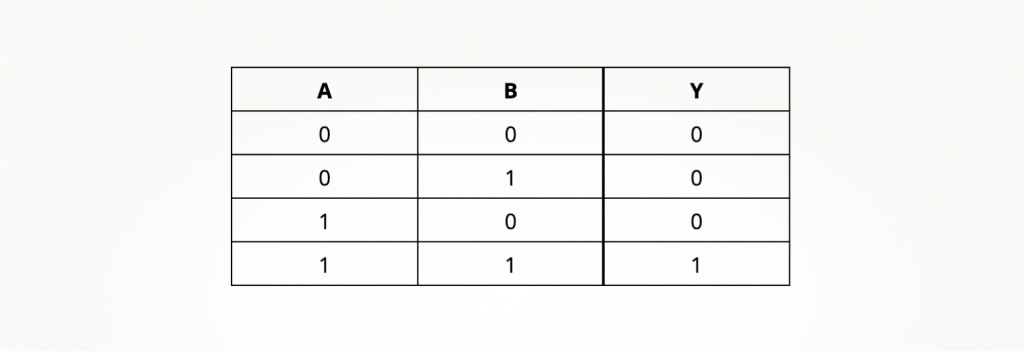
В схеме больше входов, чем у инвертора, так что количество возможных комбинаций их состояний увеличилось. Последняя строка демонстрирует: логической единицы на одном входе недостаточно для единицы на выходе. Как изготовить этот вентиль из транзисторов, расскажем позже.
Логическое И обозначается знаком умножения: А x B = Y. Другой вариант, заимствованный у программистов, — знак амперсанд: А & B = Y. На электронных схемах и в формулах можно встретить оба варианта.
Логическое ИЛИ
А теперь мы разрабатываем систему безопасности для двухкомнатной квартиры. В каждой комнате есть датчик движения, на случай если в отсутствие хозяев кто-то проберется в помещение. Какой из датчиков установил, что в квартире кто-то есть, неважно. Сигнал о вторжении нужно отправить охране в любом случае: когда движение обнаружено в первой комнате ИЛИ во второй.
Вентиль «логического ИЛИ», или OR, обозначается так:
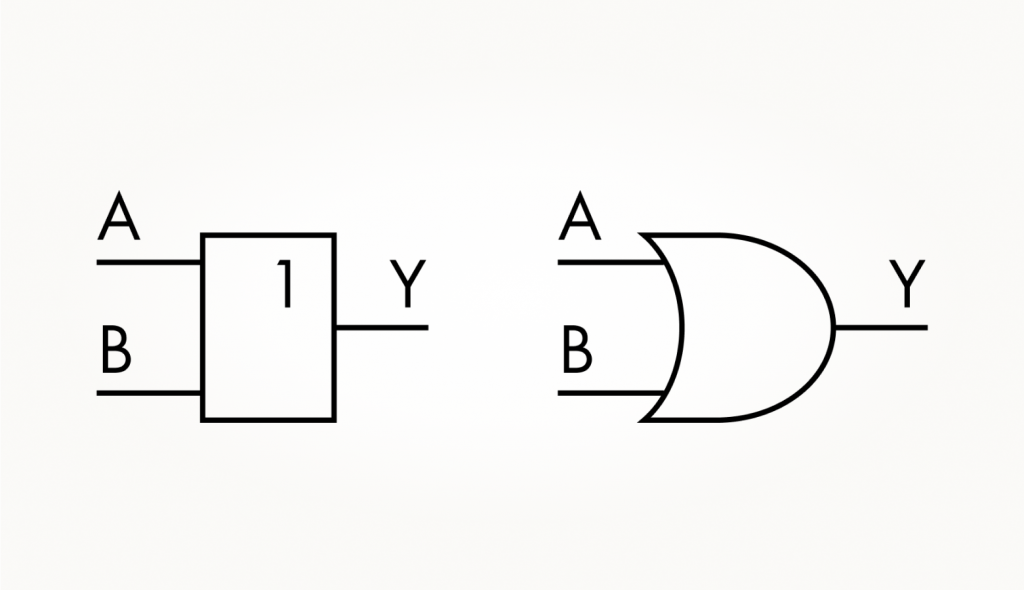
В таблице истинности тоже изменения. Теперь при единице на одном из входов мы обязательно получаем единицу на выходе:
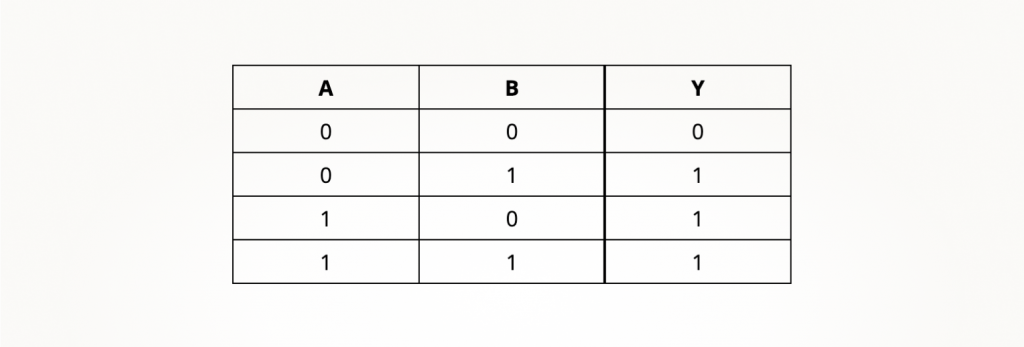
Логическое ИЛИ сигналов записывается как операция сложения: A + B = Y.
Вентиль ИЛИ-НЕ
Продолжим искать примеры вокруг, в различной бытовой технике. Вспомним о работе стиральной машинки. Ее дверцу НЕ открыть, если внутри барабана есть вода ИЛИ он крутится. В этом случае нужен логический вентиль, который выдает единицу только тогда, когда на обоих входах нули. Он есть и называется ИЛИ-НЕ (иначе — NOR). Его графическое изображение — это вентиль ИЛИ с кружком, обозначающим инверсию выхода.
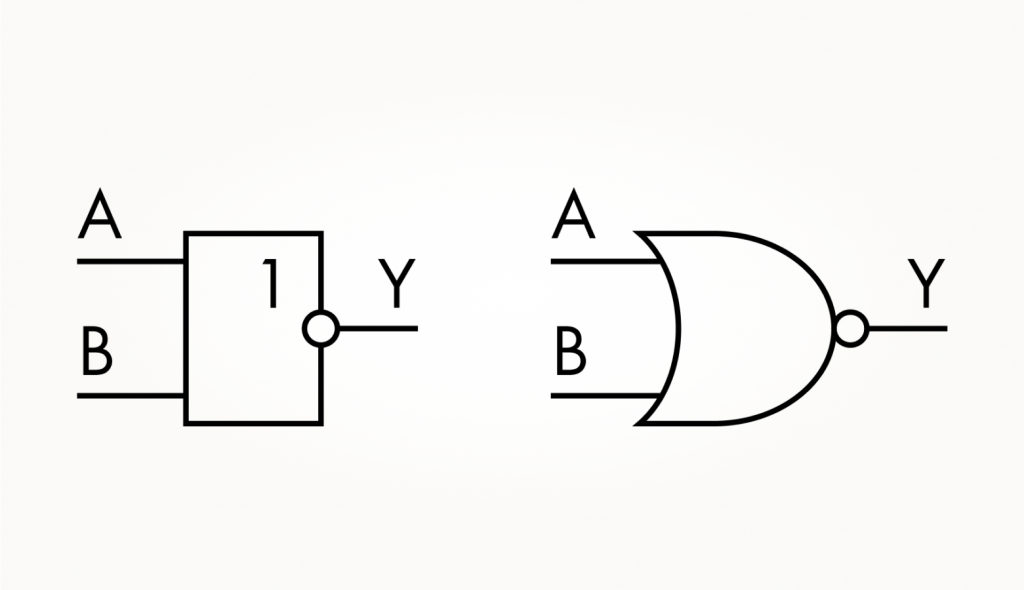
1. Попробуйте самостоятельно составить таблицу истинности для вентиля ИЛИ-НЕ.
Ответы на задания будут даны в конце статьи.
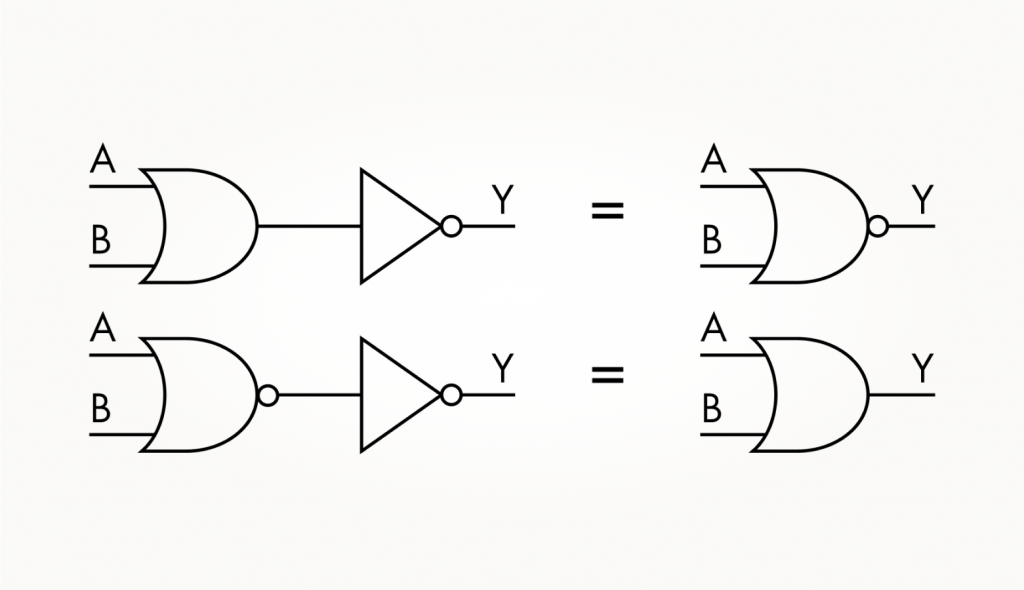
К слову, вам уже знакомо устройство, которое превращает сигналы в противоположные. Это инвертор, или логическое НЕ (NOT). Как мы уже поняли, логический вентиль ИЛИ-НЕ может быть получен из ИЛИ за счет добавления инвертора. Может быть и обратная «трансформация»: с инвертором легко получить ИЛИ из ИЛИ-НЕ. Посмотрим на эти превращения в схемах:
Вентиль И-НЕ
Чтобы продемонстрировать работу этого вентиля, давайте немного пофантазируем. Допустим, у нас есть дата-центр, который должен работать непрерывно, 24/7. Отключить электропитание в нем можно, только если нажать сразу на две кнопки: одна — у руководителя системных инженеров дата-центра, а вторая — у его технического директора. Получается, дата-центр НЕ будет работать, только если руководитель системных инженеров И технический директор нажмут на кнопки отключения электричества.
В такой системе реализовывается функция логического И-НЕ, или NAND. Графически такой вентиль обозначается следующий образом:
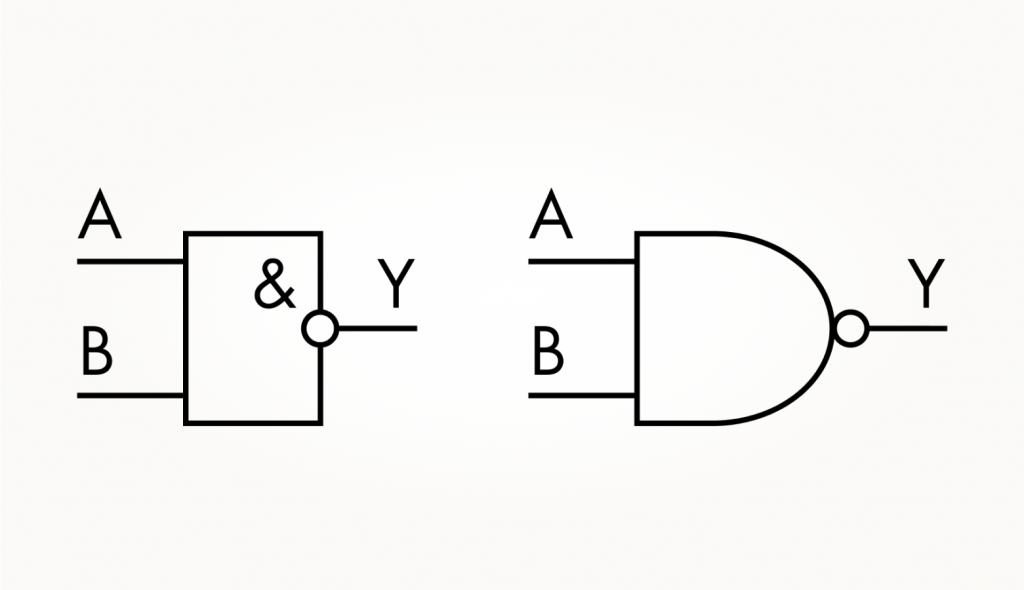
Помните, как выглядят формулы для И и ИЛИ? Там участвовали знакомые нам знаки сложения и умножения. Чтобы отразить НЕ в формуле, нужно добавить черту инверсии над всей формулой сложения или умножения входных сигналов.
Например:
2. Cоставьте таблицу истинности логического И-НЕ.
3. Нарисуйте схемы преобразования вентиля И в И-НЕ и наоборот.
4. Каким будет состояние выхода, если на один вход ИЛИ-НЕ подается логическая единица, а на другой — логический ноль?
5. Что будет на выходе схемы из двух инверторов, подключенных друг за другом? То есть чему будет равна двойная инверсия сигнала?
Ответы вас ждут в ниже в статье.
Исключающее ИЛИ и Исключающее ИЛИ-НЕ
Рассмотрим еще один, последний в этой статье, важный логический вентиль — Исключающее ИЛИ (XOR). По сути, он помогает в сравнении данных: этот вентиль выдает ноль, если сигналы на входах одинаковые, и единицу, если разные.
Графически этот вентиль обозначается так:
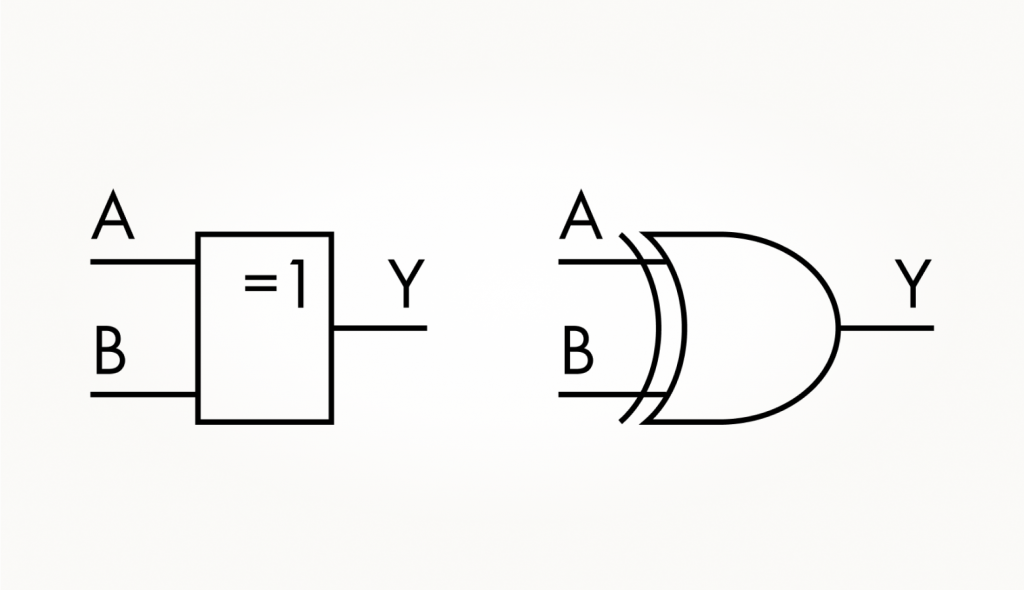
А вот таблица истинности вентиля:
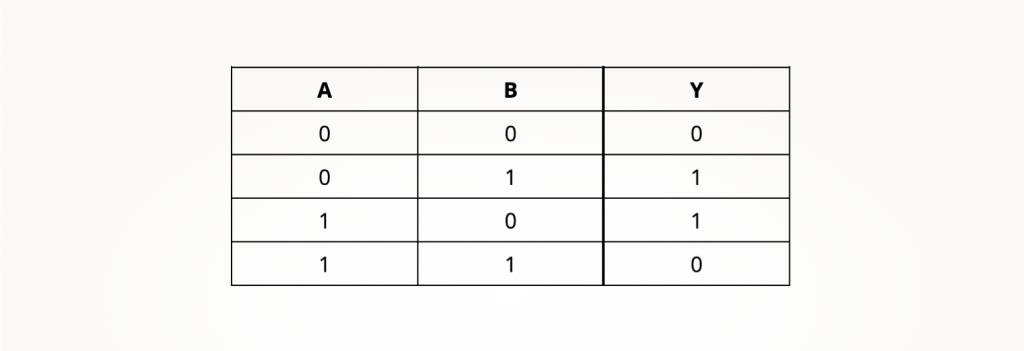
Помимо Исключающего ИЛИ, есть и Исключающее ИЛИ-НЕ (на английском языке обозначается как XNOR). С графическим обозначением вентиля все просто — просто добавляем к обозначению Исключающего ИЛИ кружок, обозначающий инверсию.
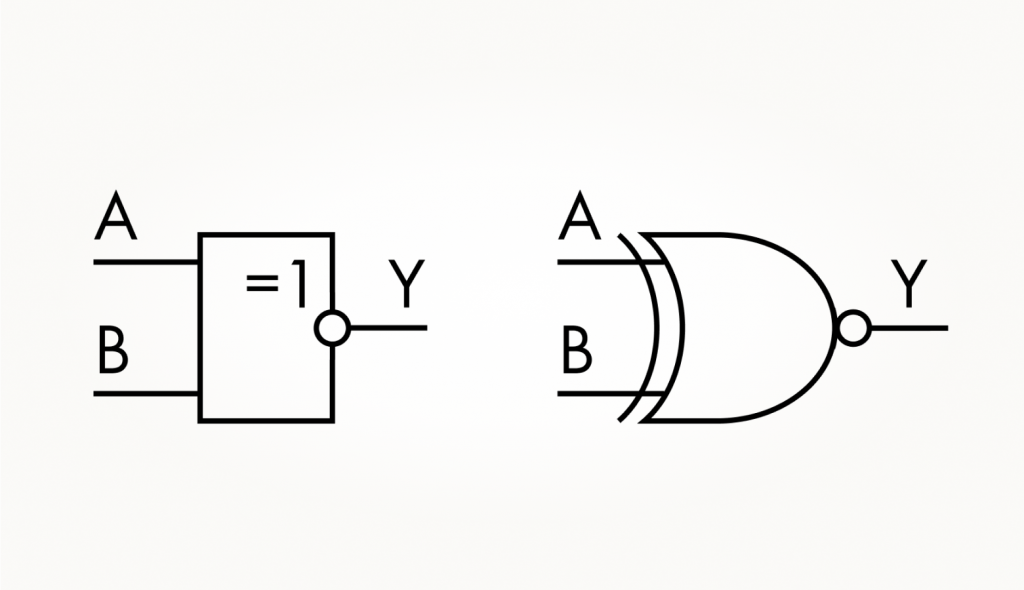
Ну и по традиции — таблица истинности для Исключающего ИЛИ-НЕ:
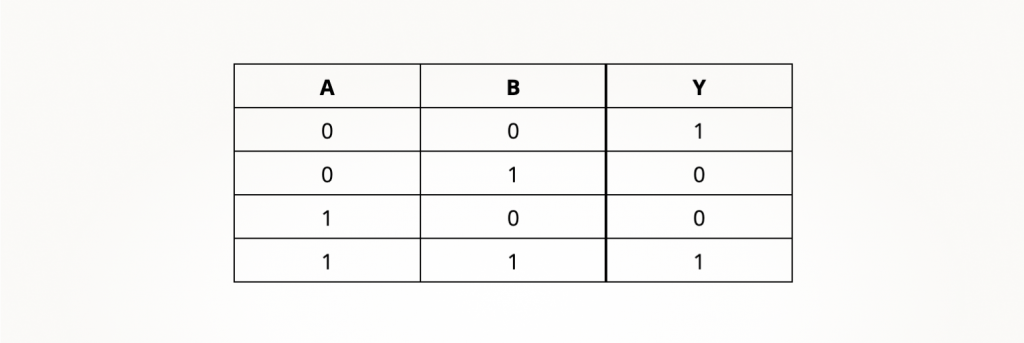
Если вы решили последнее задание для самопроверки, то знаете, что двойная инверсия сигнала равняется самому сигналу (инверсия единицы — это ноль, а инверсия нуля — это единица). А еще вы знаете, что с помощью инвертора можно преобразовать функцию И в И-НЕ (а ИЛИ в ИЛИ-НЕ). Но булева алгебра позволяет выполнять и более сложные преобразования, о которых вы обязательно узнаете, если в будущем будете изучать этот раздел математики.
Конструируем базовые логические элементы: от таблиц истинности к схемам на транзисторах
Итак, мы рассмотрели логические вентили и их функции. Теперь давайте поймем, как воплотить их физически, собрав на макетной плате.
Возможно, когда вы смотрели на схемы вентилей, задавались вопросом, почему они содержат только контакты для входных и выходных сигналов. Где же контакты с шинами питания? Вопрос справедливый, но эти обозначаются опускаются для упрощения. Считается, что инженер-схемотехник точно не забудет подключить вентили к питанию.
Практическая схема И-НЕ на транзисторах
Учиться создавать транзисторные схемы проще всего с вентиля И-НЕ. Составили ли вы для него таблицу истинности — одно из заданий для самопроверки? Давайте сравним реальность с тем, что у вас получилось.
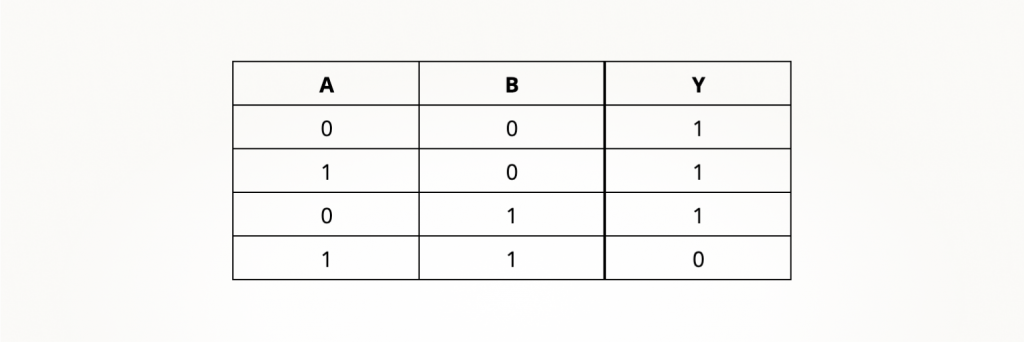
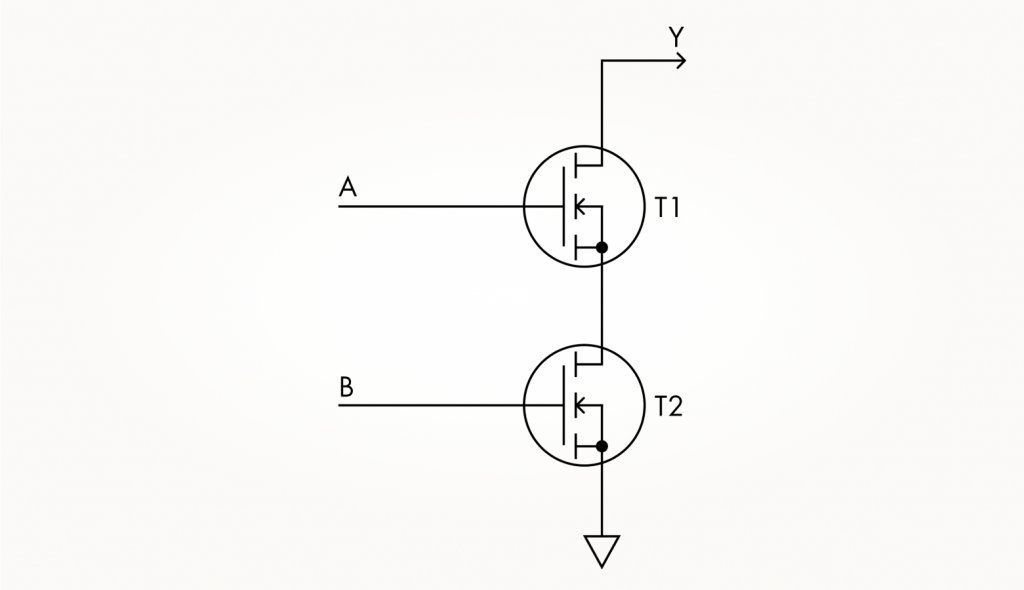
Как вы уже знаете, логический ноль на выходе КМОП-схем без потерь создается n-канальными транзисторами. Из таблицы видно, что ноль появляется только в одном случае: когда на оба входа одновременно подается логическая единица. Такое поведение можно обеспечить, установив два n-канальных транзистора друг за другом, то есть последовательно. В таком случае единица на любом входе — A или B — будет открывать только свой транзистор, а ток от выхода Y к минусу питания потечет, лишь когда сразу два транзистора будут открыты. Вот так будет выглядеть эта цепочка:
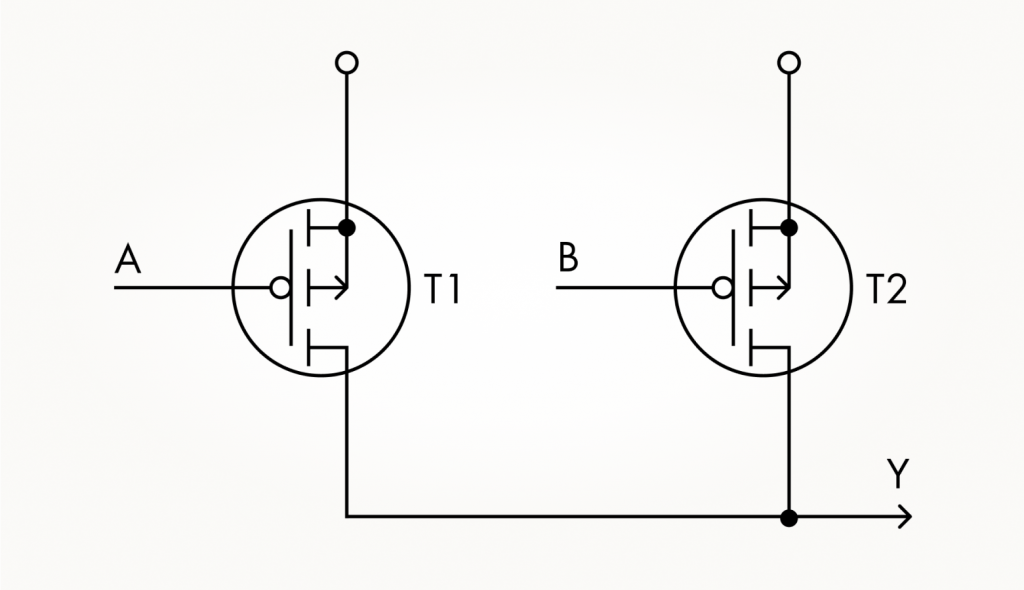
Теперь нужно в таблице истинности найти, при каких условиях на выходе Y появляется логическая единица. Для этого любой из входных сигналов должен быть равным нулю. Транзистор, открывающийся нулем и передающий единицу на выход, — это p-канальный прибор. Чтобы реализовать нужное поведение вентиля, два транзистора должны быть подключены параллельно, то есть их стоки объединяются на выходе Y, а истоки — на плюсе питания, как на схеме ниже. Тогда ноль на любом из входов откроет свой p-канальный транзистор, и ток потечет между плюсом батареи питания и выходом Y.
Соединив полученные цепочки p- и n-канальных транзисторов в одну, получаем вот такую схему вентиля И-НЕ:
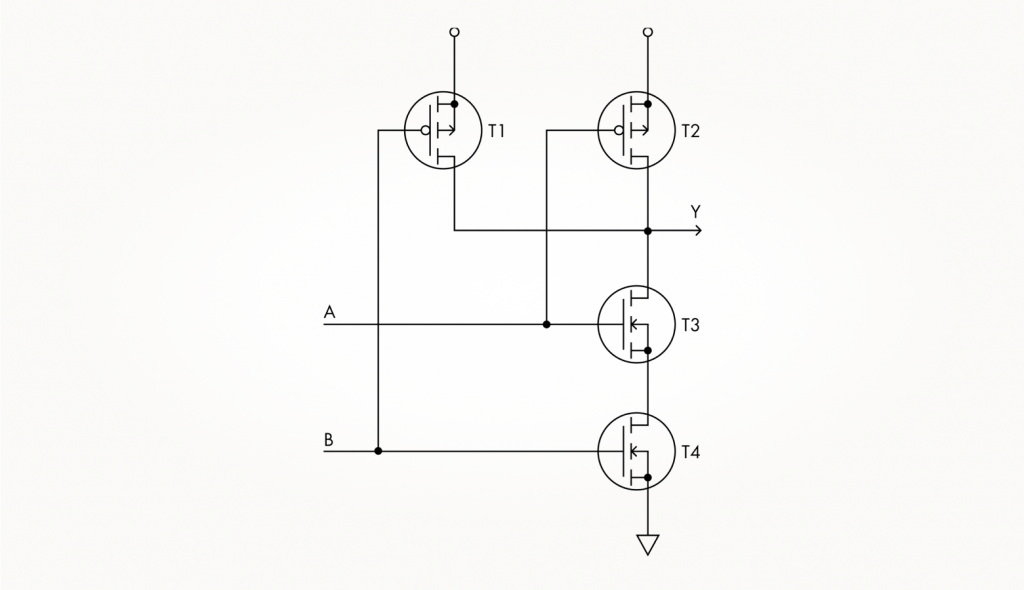
Если вы внимательно посмотрите на таблицу истинности И-НЕ и на полученную схему, то увидите, что входы A и B равнозначны. Даже если поменять их местами, с точки зрения выполняемой функции работа вентиля никак не изменится. Дальше вы поймете, что это замечание справедливо и для остальных вентилей, с которыми мы познакомились в этой главе.
Алгоритм создания цифровых логических схем на транзисторах
Итак, еще раз по шагам рассмотрим процесс создания, или синтеза, схемы на транзисторном уровне по таблице истинности.
- Определяем, какая комбинация входных сигналов должна приводить к появлению единицы на выходе. Эту электрическую цепь схемы нужно реализовывать на p-канальных транзисторах.
- Определяем, какая комбинация входных сигналов должна приводить к появлению нуля на выходе. Эту цепь надо реализовывать на n-канальных транзисторах.
- Если нужный сигнал на выходе появляется, только когда ВСЕ или несколько входных сигналов цепи требуют этого, то цепь схемы составляем из последовательно включенных транзисторов.
- Если нужный сигнал на выходе появляется, даже когда ЛЮБОЙ из нескольких входных сигналов требует этого, то цепь схемы составляем из параллельно включенных транзисторов.
6. Прежде чем двигаться дальше, попробуйте самостоятельно создать схему ИЛИ-НЕ по таблице истинности.
Практические схемы вентилей И и ИЛИ на транзисторах
Если вспомнить про взаимное преобразование ИЛИ-НЕ и ИЛИ с помощью инвертора, то, добавив по одному n- и p-канальному транзистору в схему ИЛИ-НЕ, легко получить вентиль ИЛИ.
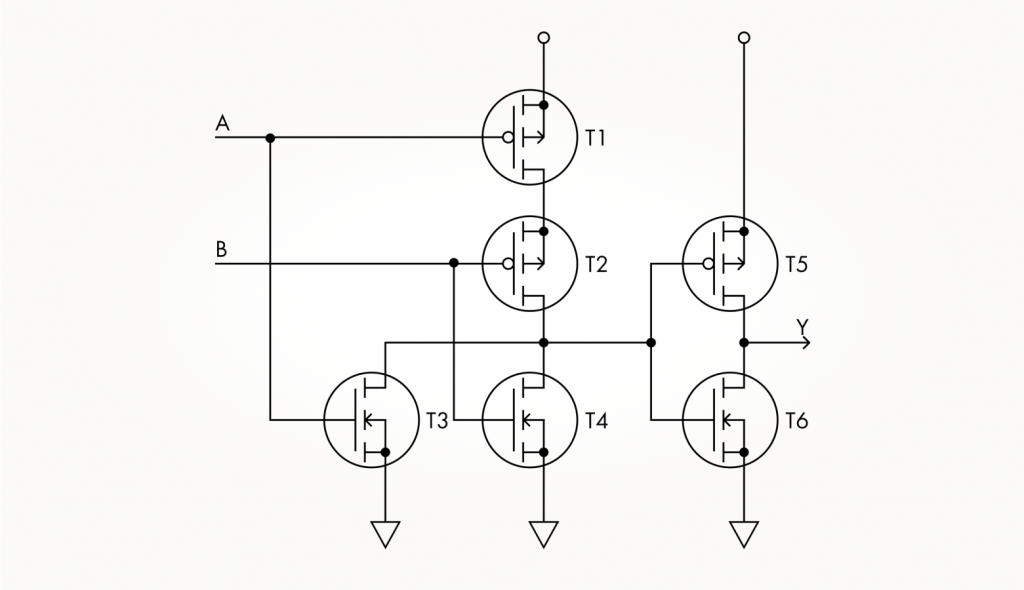
То же самое справедливо и для логического И:
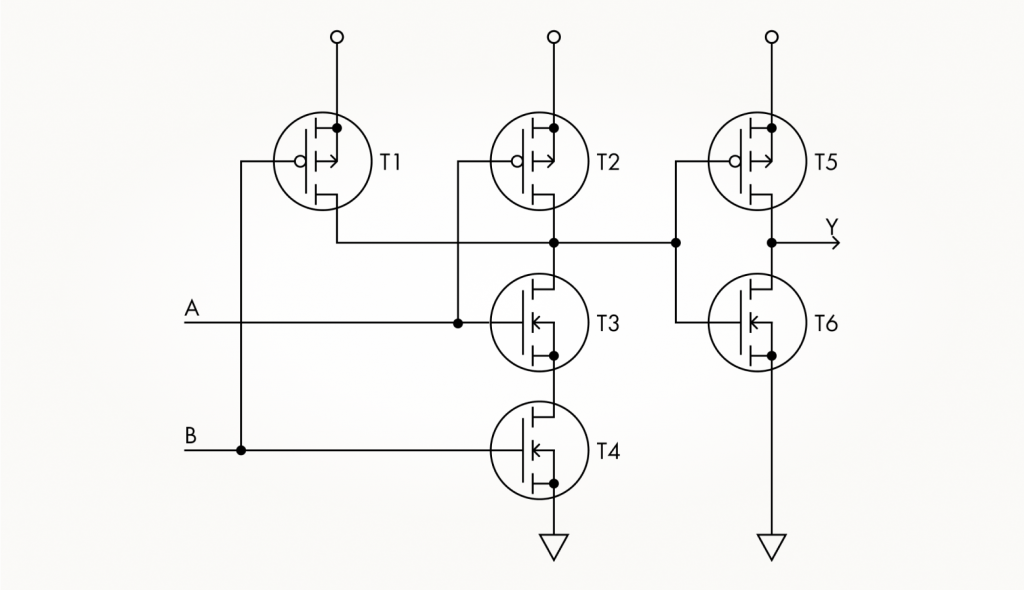
Именно такие схемы используются для реализации логических вентилей в КМОП микросхемах.
Хорошо бы для практики собрать рассмотренные вентили на макетной плате и проверить их работу. Попробуйте, это совсем не трудно!
Практическая схема Исключающего ИЛИ на транзисторах
Из базовых элементов мы не рассмотрели только схему Исключающего ИЛИ — не самую простую. Существует несколько вариантов ее создания с разным количеством транзисторов.
Не лишним будет вспомнить таблицу истинности вентиля.
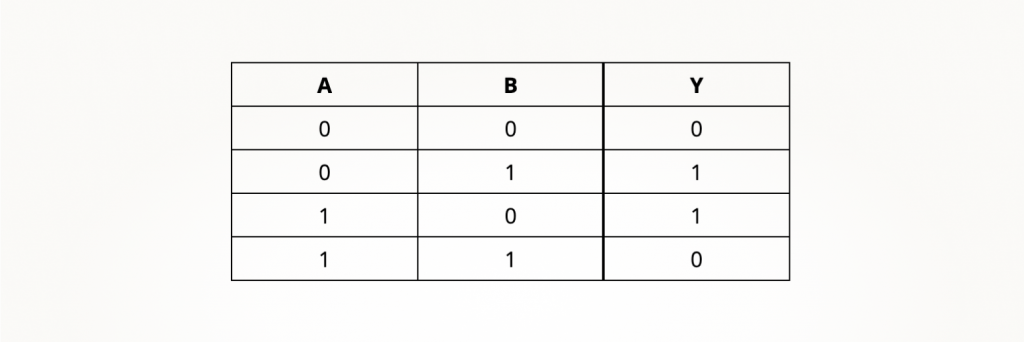
Рассмотрим классический способ создания схемы Исключающего ИЛИ. Единица на выходе появляется в случае, когда A = 0 и B = 1 или A = 1 и B = 0. Сразу возникает вопрос, как реализовать эту цепь схемы на p-канальных транзисторах, которые открываются логическим нулем, если у нас один из сигналов обязательно будет единицей. Не лучше ситуация и с n-канальной цепью, которая должна активироваться при A = 0 и B = 0 или A = 1 и B = 1. Если со вторым условием все понятно, то первое не реализовать на приборах, которые открываются логической единицей.
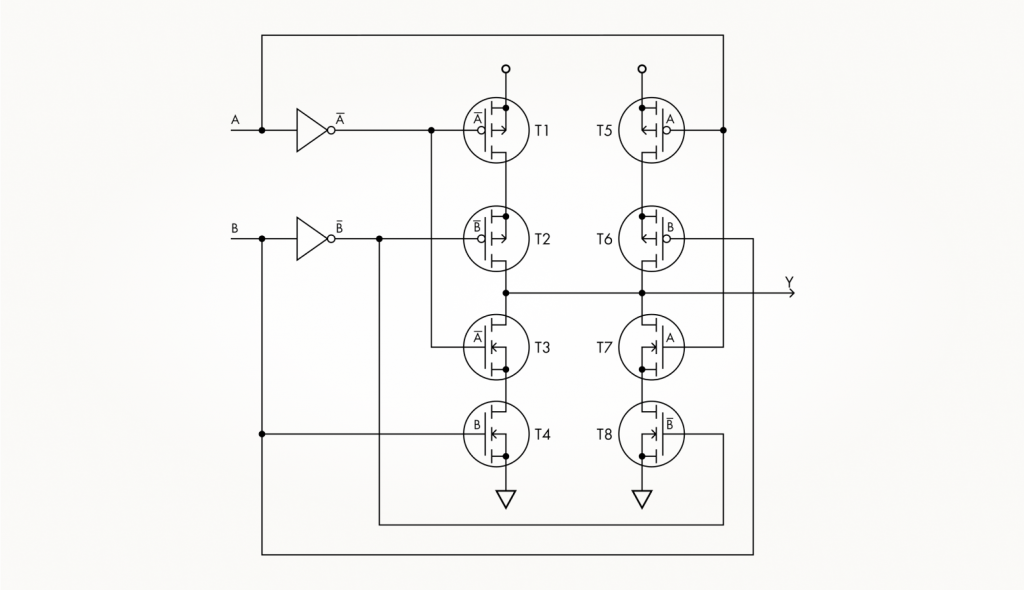
Выход из затруднительной ситуации следующий: нужно инвертировать входные сигналы и подавать на затворы транзисторов прямой или инверсный сигнал в зависимости от требуемой ситуации. Тогда схема вентиля Исключающее ИЛИ будет выглядеть так:
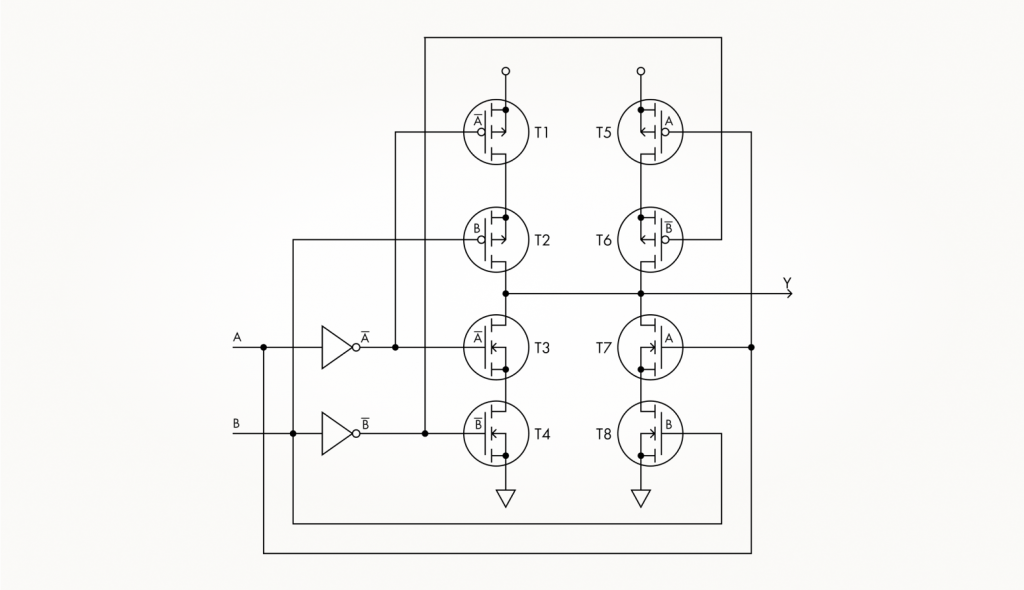
Здесь каждой из четырех возможных комбинаций входных сигналов соответствует одна цепочка из двух последовательно соединенных транзисторов: Т1 и Т2 открываются при A = 1 и B = 0, Т3 и Т4 — при A = 0 и B = 0, Т5 и Т6 — при A = 0 и B = 1, Т7 и Т8 — при A = 1 и B = 1. Так реализуется таблица истинности Исключающего ИЛИ.
Схема, воспроизводящая Исключающее ИЛИ на макетной плате, занимает немало места. Тот варианта, что показан на фото ниже, собирался на другом представителе семейства n-канальных транзисторов, а не тех BS-170, что используются в практической части нашего курса. У этих транзисторов несмотря на тот же корпус иной порядок расположения выводов, поэтому слепо копировать ее с фото на макетную плату не стоит. Фотография иллюстрирует сложность подобных схем на дискретных компонентах. А ведь это всего лишь одни вентиль! Транзисторы, образующие инверторы на входах A и B, притаились в правом нижнем углу платы, недалеко он проводов питания. Батарейка в кадр не вошла.

В отличие от способа получения ИЛИ из ИЛИ-НЕ Исключающее ИЛИ-НЕ не требует добавления транзисторов на выход схемы. Достаточно перераспределить сигналы, приходящие на затворы приборов c T1 по T8, чтобы реализовать ее на тех же двенадцати транзисторах.
7. Попробуйте самостоятельно создать схему Исключающего ИЛИ-НЕ на базе Исключающего ИЛИ и собрать ее на макетной плате.
Добавляем входы в логические схемы
До сих пор мы рассматривали вентили, которые получают сигналы из двух источников, то есть двухвходовые схемы (А и B). Но как быть, если нужно объединить функцией И-НЕ три входа? Да все так же! Начинаем с таблицы истинности — возможных комбинаций входов будет уже восемь. Наверно, вы уже обратили внимание, что в ячейках, соответствующих входам A, B, C сверху вниз в строках таблицы идет перебор двоичной записи чисел от 0 до 7 по порядку. Так делать не обязательно, но это очень удобно и помогает не забыть никакое из значений или не написать дважды одно и то же пропустив какое-то нужное.
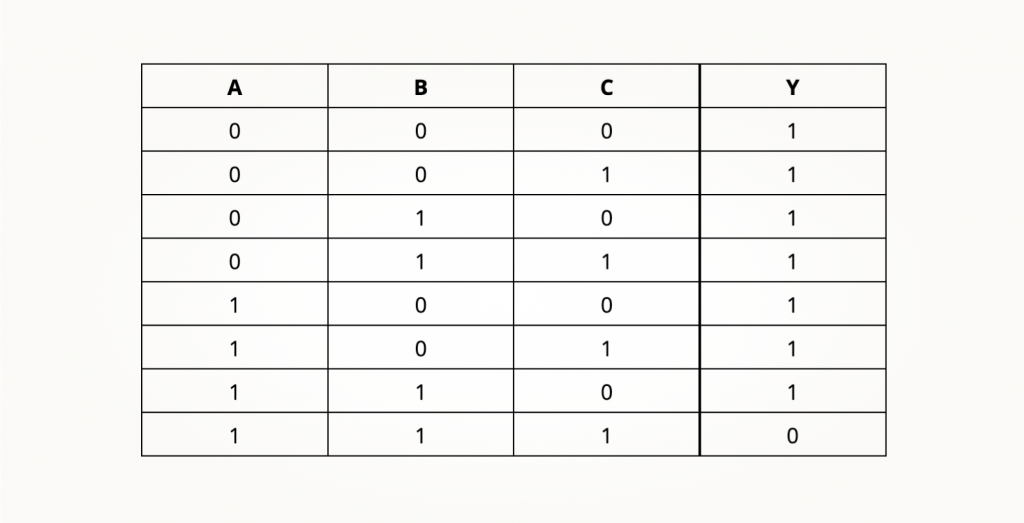
В соответствии с этой таблицей и алгоритмом синтеза вентилей добавим в схему еще два транзистора. Условное обозначение такого элемента выглядит так:
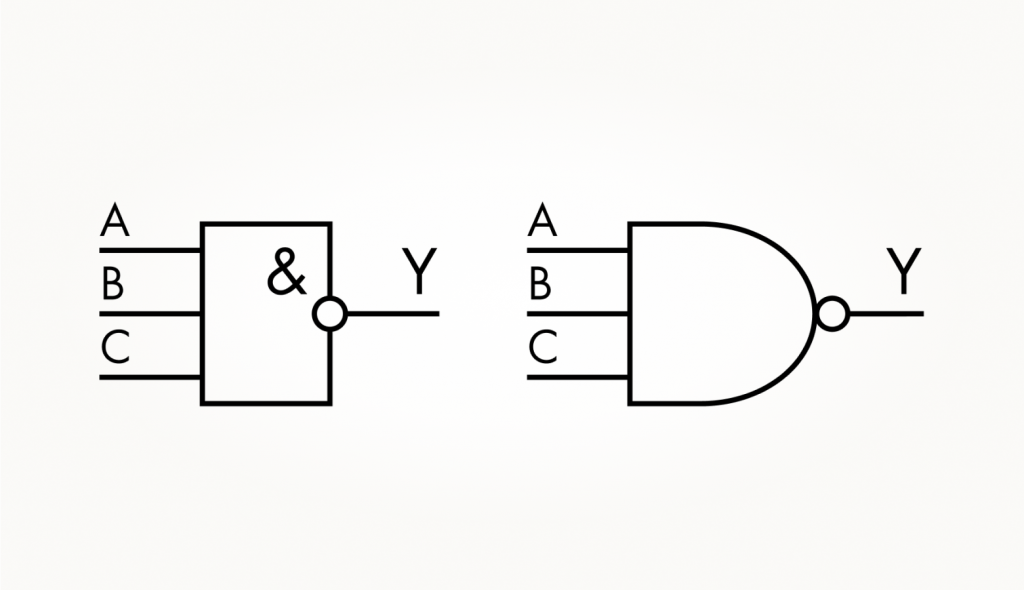
Чтобы отличить друг от друга вентили, у которых одна логическая функция, но разное число входов, в их наименование добавляют цифру, соответствующую числу входов. При этом в отечественных обозначениях эту цифру добавляют в начале, например, 3И-НЕ. А в зарубежных — в конце: NAND3. А вот с обозначением в имени вентиля инверсии выхода, если она есть, как вы могли заметить, все ровно наоборот. Уж такие разные традиции сложились!
Вот так выглядит схема элемента 3И-НЕ:
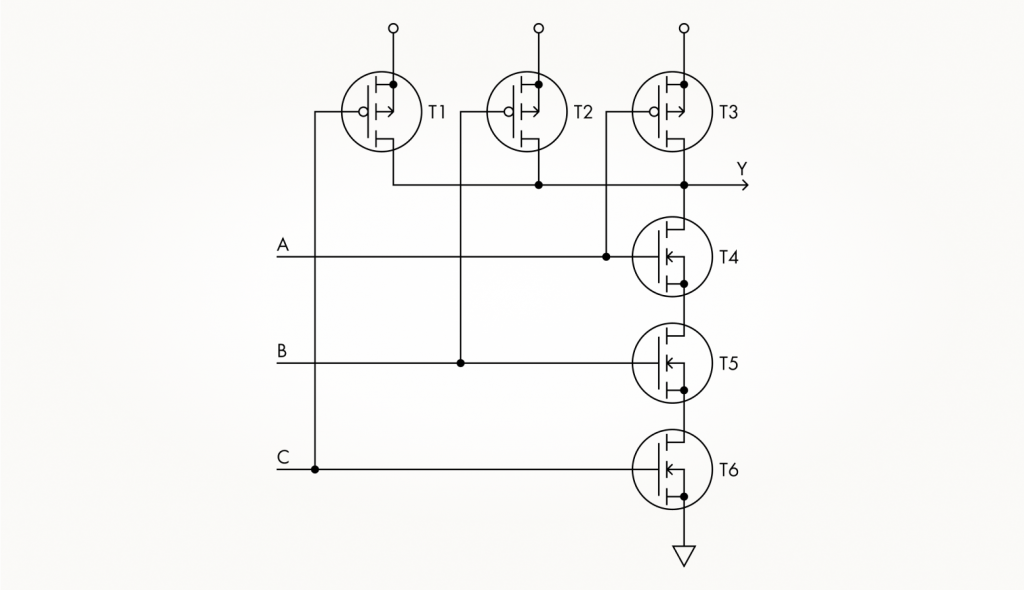
Аналогичным образом можно получить и схемы 3И, 3ИЛИ, 3ИЛИ-НЕ на основе ранее рассмотренных схем с двумя входами. Также можно добавить больше входов, но на практике больше четырех входов в таких вентилях не применяется. Цепочка из большого количества последовательно включенных транзисторов переключается слишком медленно, чтобы ее можно было использовать в быстродействующих системах. А вентили типа Исключающего ИЛИ вообще используются только двухвходовые.
Посмотрите ролик, чтобы увидеть, как ведут себя некоторые рассмотренные в этой статье вентили, собранные на транзисторах.
Ответы на вопросы для самопроверки
1. Таблица истинности для вентиля ИЛИ-НЕ.
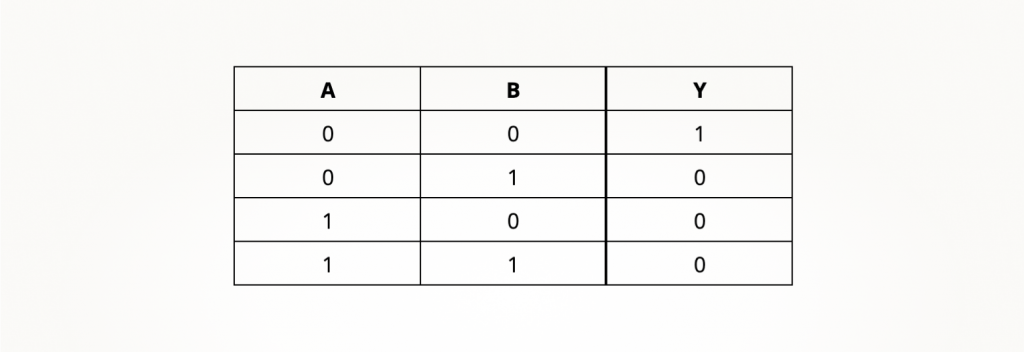
2. Таблица истинности логического И-НЕ.
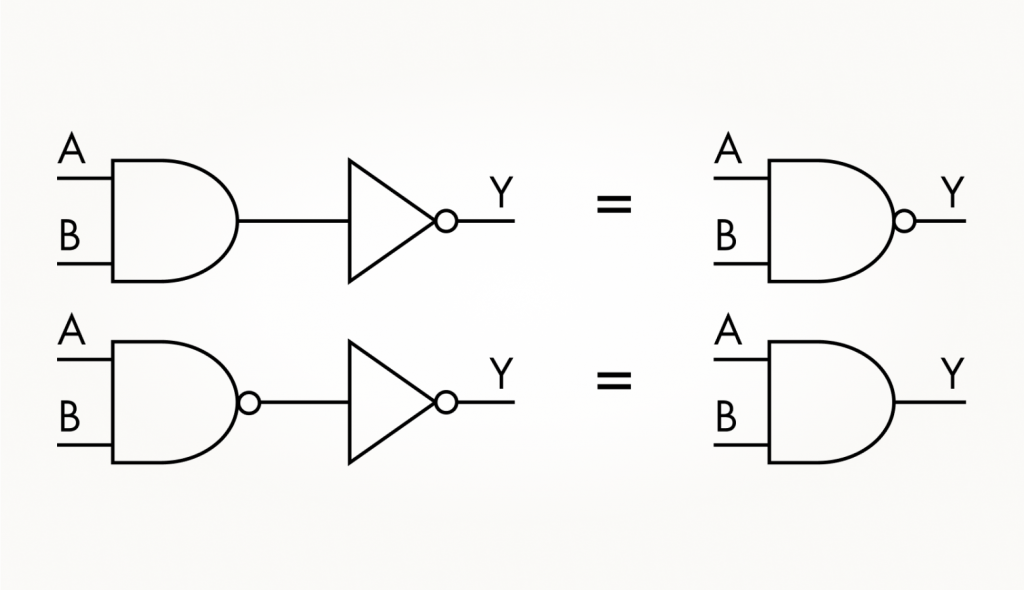
3. Схемы преобразования вентиля И в И-НЕ и наоборот.
4. Если на один вход ИЛИ-НЕ подается логическая единица, а на другой — логический ноль, состояние выхода будет 0.
5. Двойная инверсия сигнала будет равна самому сигналу. Легко проверить. Если мы инвертируем ноль один раз, то получим единицу. Вторая инверсия превратит единицу обратно в ноль. То же самое справедливо и для двойной инверсии единицы.
6. Схема ИЛИ-НЕ.
7. Схема Исключающего ИЛИ-НЕ на базе Исключающего ИЛИ.

Здравствуйте подскажите пожалуйста пересмотрела кучу роликов и сижу уже второй день не могу собрать логическое НЕ в proteus
n-mop все понятно на исток минус по схеме тоже землю подтягивем к истоку как раз n-mop у нас внизу, НО как быть с р-mop он у нас в самом верху и его сток идет к источнику напряжения так не работает ведь, а если там р-mop с защитным диодом тогда ток всегда через него будет протекать без разницы что на управляющем сигнале логический 0 или 1
Подскажите как это понять логикак в логике не работает
Здравствуйте, Валерия! К плюсу питания должен быть обращен ИСТОК p-канального транзистора, а не СТОК. Это подробно изложено в теоретическом материале выше (см. пункты «чтобы получить схему универсального индикатора двоичных сигналов, нам нужно…»)
Добрый день! Нашла опечатку в последне строке таблицы истинности для вентиля ИЛИ-НЕ. 1 NOR 1 должно равняться 0
Уточните, пожалуйста, что имеете в виду. Сейчас в статье так и написано: ИЛИ-НЕ при А=1 и В=1 на выходе Y должен быть 0.Или вы имеете в виду «Исключающее ИЛИ-НЕ»? Это уже другой элемент, у него другая таблица истинности.