программы

Математика матричных расширений: умножение матриц на примере T-Head Matrix Extension

309

7 августа 2024

Изображение создано с помощью нейросети

программы

309

7 августа 2024

Математика матричных расширений: умножение матриц на примере T-Head Matrix Extension

В заключительной статье цикла про матричные расширения инженер-программист Андрей Соколов разберет пример использования T-Head Matrix Extension под RISC-V для реализации алгоритма матричного умножения. Сначала вы кратко рассмотрите наивную скалярную реализацию и блочный вариант алгоритма. Затем реализуете аналогичный вариант с использованием матричного расширения — как для квадратных матриц, так и матриц произвольного размера. А в заключение Андрей расскажет, какие идеи можно использовать для дальнейшей оптимизации матричного умножения, и поделится полезными ссылками.

Изображение создано с помощью нейросети

Из статьи вы узнаете

Как выглядит наивная скалярная реализация и блочный вариант алгоритма
реализуем аналогичный вариант с использованКак реализовать матричное расширение для квадратных матриц
Что делать, если матрицы произвольного размера
Какие идеи можно использовать для дальнейшей оптимизации матричного умножения

Статья не показывает пошаговую оптимизацию умножения матриц для достижения максимума FLOPS и не учит, как писать вычислительные ядра на ассемблере. Но демонстрирует использование матричного расширения и основные идеи оптимизации матричного умножения.

Работа с эмулятором

Пока независимое матричное расширение от компании T-Head не реализовано в железе. Единственная возможность запустить код с матричными инструкциями — использовать симулятор, в нашем случае QEMU. Он позволяет запускать RISC-V-код на x86-архитектуре. Помимо этого, понадобится RISC-V тулчейн для сборки. На GitHub компании T-Head можно найти все необходимое: скачать GCC тулчейн для кросс-компиляции и QEMU.

Для удобства работы с матричным расширением наша команда в YADRO сделала отдельный репозиторий на GitHub с удобной настройкой окружения, сборкой и запуском тестов на QEMU. Он содержит библиотеку со своими тестами и CI. Не хватает только тестов производительности, но для QEMU они бессмысленны.

Для работы с репозиторием нужно выполнить несколько шагов:

Настроить окружение с помощью скрипта env.sh.
Собрать проект с помощью скрипта build.sh.
Запустить на QEMU.

./tools/qemu/bin/qemu-riscv64 -cpu c907fdvm-rv64 ./_build/test/test_rvm_square

где c907fdvm-rv64 — эмуляция CPU с поддержкой матричного расширения.

Весь код из этой статьи можно найти в указанном репозитории. Кроме того, он будет полезен для самостоятельной практики: вы можете попробовать реализовать более эффективную версию матричного умножения, для другого типа данных, а также добавить реализации для других алгоритмов линейной алгебры.

После подготовки репозитория и серии статей вышла новая версия API интринсиков для матричного расширения.

Основные отличия — в изменении префикса в названиях и добавлении размеров блоков в аргументы функций. В этой статье мы рассмотрим старую версию, но обновленную реализацию можно посмотреть в отдельной ветке нашего репозитория. Для сборки нужно скачать более новый тулчейн версии 2.10.1 с сайта Xuantie (для скачивания нужно зарегистрироваться).

Скалярная версия умножения матриц

В отличие от GEMM (GEneral Matrix Matrix multiplication) из BLAS-функциональности, наша версия умножения матриц будет без скалярных коэффициентов alpha и beta, а также без аргументов lda, ldb и ldc.

Начнем мы с самого наивного алгоритма с тремя циклами:

void gemm_ref(const float *A, const float *B, float *C, const size_t n, const size_t m, const size_t k)
{
    for (size_t i = 0; i < n; i++) { /* Loop over the rows of C */
	    for (size_t j = 0; j < k; j++) { /* Loop over the columns of C */
	        for (size_t p = 0; p < m; p++) {  /* Update C( i,j ) with the     inner
	                                             product of the ith row of A and
	                                             the jth column of B */
	            C[i * k + j] += A[i * m + p] * B[p * k + j];
	        }
	    }
    }
}

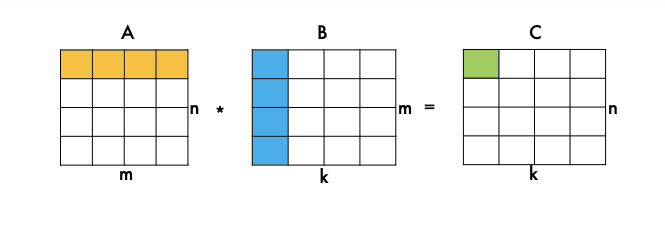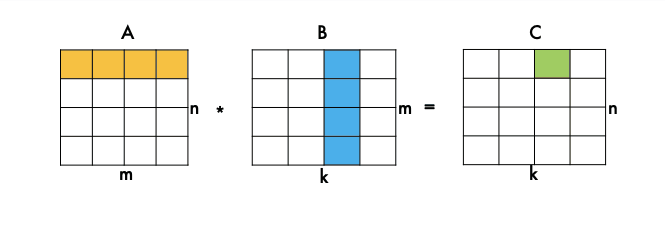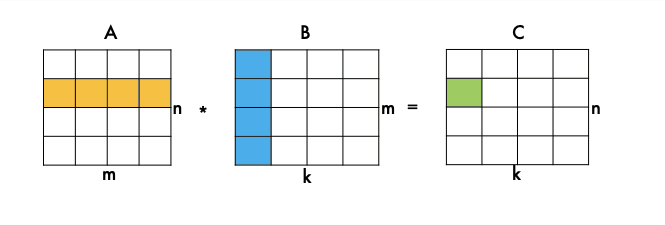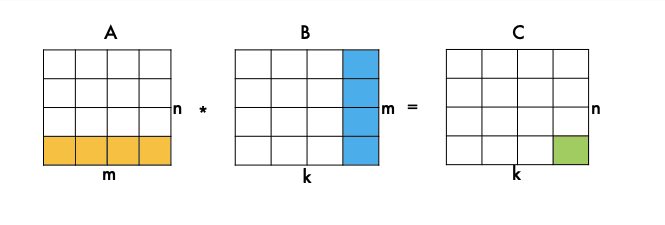
Первые два цикла — это итерация по матрице C, мы ходим по каждому элементу, а третий цикл — это скалярное произведение вектора строки, А на вектор столбца B. Параметры — это указатели на матрицы A, B и C и три размерности перемножаемых матриц.

Мы идем по элементам матрицы C и вычисляем одно скалярное произведение.

Но, конечно, эта реализация работает очень медленно. Более быстрые основаны на блочном алгоритме умножения матриц.

#define BLOCK_SIZE 4
 
static inline void process_block_4x4(const size_t m, const float *A, const size_t lda, const float *B, const size_t ldb, float *C, const size_t ldc) {
    for (size_t i = 0; i < BLOCK_SIZE; i += 1) {
        for (size_t j = 0; j < BLOCK_SIZE; j += 1) {
            for (size_t p = 0; p < m; p += 1) {
                C[(j * ldc) + i] += A[(j * lda) + p] * B[(p * ldb) + i];
            }
        }
    }
}
 
void gemm_block4x4_ref(const float *A, const float *B, float *C, const size_t n, const size_t m, const size_t k)
{
    for (size_t j = 0; j < k; j += BLOCK_SIZE) { /* Loop over the columns of C */
        for (size_t i = 0; i < n; i += BLOCK_SIZE) { /* Loop over the rows of C */
            process_block_4x4(m, &A[i*m], m, &B[j], k, &C[(i*k) + j], k);
        }
    }
}

Тут уже знакомые нам циклы, только итерируемся мы теперь не по элементам матрицы С, а по ее блокам. А уже в функции process_block₄×4() выполняется вычисление одного блока матрицы C. В функцию передаются:

размерность m — длина скалярного произведения,
A, B, C — указатели на блоки матриц,
lda, ldb и ldc — leading dimension, количество элементов до следующей строки матрицы.

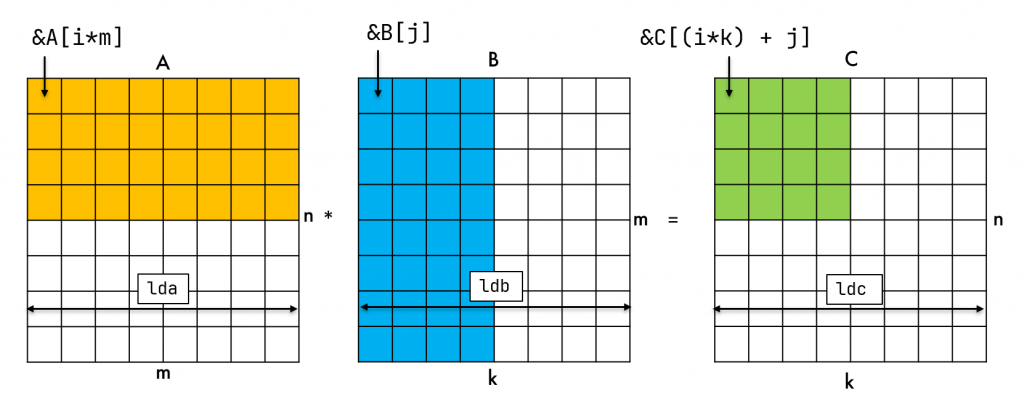
Может возникнуть вопрос: нужен ли такой блочный алгоритм и в чем его преимущество перед наивным алгоритмом. Показательный ответ — в количестве операций загрузки. Для наивного алгоритма, чтобы посчитать одну строку матрицы C, состоящую в нашем примере из 8 элементов, нам нужна одна строка матрицы A и вся матрица B. В итоге получается 64 загрузки.

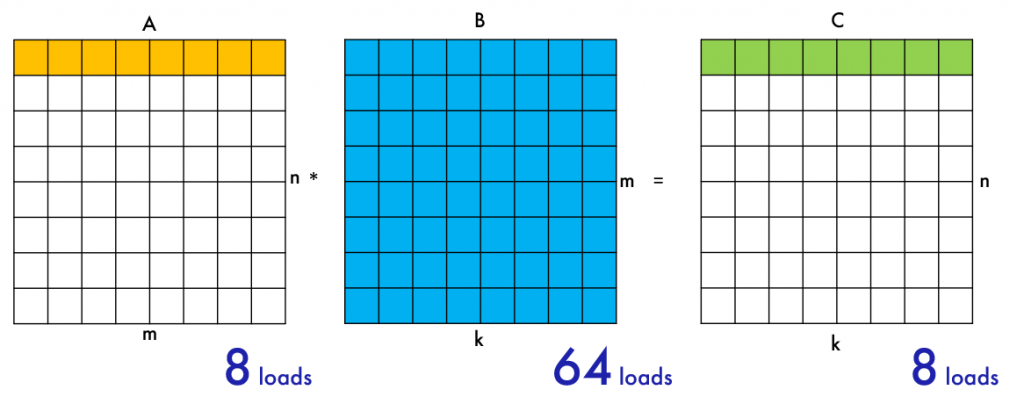
Подсчет одной строки матрицы C в случае наивного алгоритма

В случае блочного алгоритма для расчета блока матрицы С, имеющего размер 4×2 (то есть тоже из 8 элементов), нам уже нужны две строки матрицы A (16 элементов) и уже половина матрицы B. В итоге — 32 загрузки.

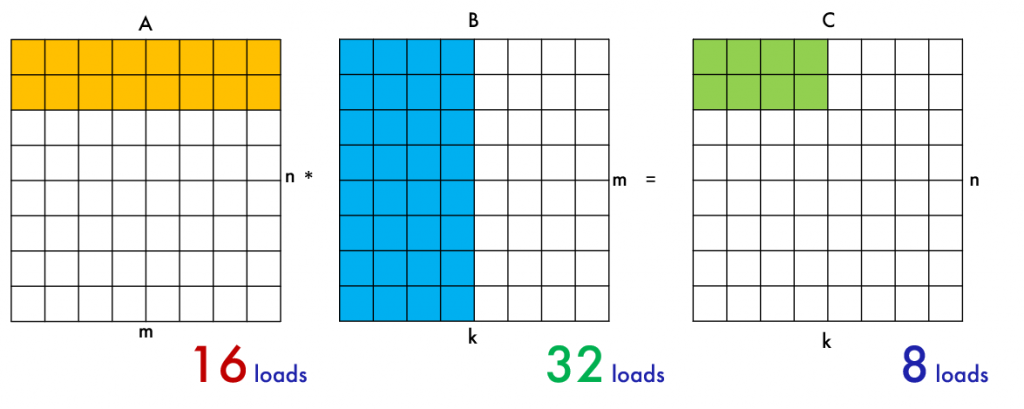
Расчет блока матрицы С в случае блочного алгоритмы

В результате для расчета одного и того же количества элементов матрицы С мы получаем 80 загрузок (наивный алгоритм) против 56 загрузок (блочный алгоритм).

Кажется, что разница не такая уж и большая, но мы рассматривали маленькие матрицы. Для больших матриц — например, со строкой С из 1024 элементов или блока 32×32 — в аналогичных подсчетах разница будет колоссальной: 1 050 624 загрузки против 66 560.

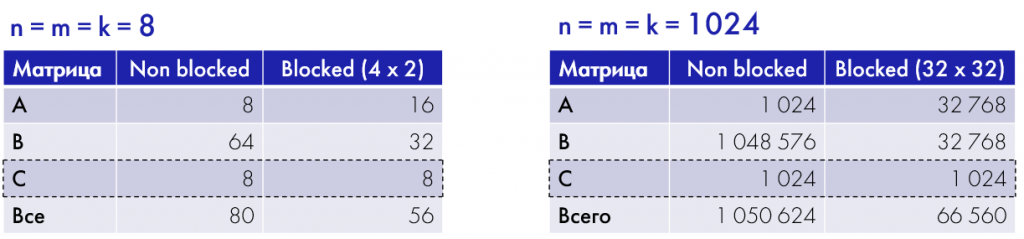
Сравнение результатов использования наивного и блочного алгоритмов в операциях над матрицами

Таким образом, за счет уменьшения количества загрузок в блочном алгоритме мы получаем большую кэш-локальность. Также он способствует эффективной векторизации и параллелизации алгоритма. Но эта версия алгоритма тоже далека от идеала.

Чтобы попрактиковаться с матричным расширением, возьмем за основу рассмотренную версию блочного алгоритма, а в конце статьи обсудим, как реализовывать умножение матриц эффективнее.

Матричная реализация алгоритма умножения матриц

Со скалярными реализациями матричного умножения мы разобрались. Теперь приступим к реализации блочного алгоритма с помощью матричного расширения. Реализация gemm_block4x4_rvm () пока аналогична скалярной версии. Итерируемся по блокам, вызываем функцию process_block₄×4(), которая полностью считает один блок матрицы C размера 4×4, передаем в нее длину скалярного произведения и уже в ней считаем 16 скалярных произведений этого блока.

#define BLOCK_SIZE 4
static inline void process_block_4x4(const size_t m,
                                     const float *A, const size_t lda,
                                     const float *B, const size_t ldb,
                                           float *C, const size_t ldc);
 
void gemm_block4x4_rvm(const float *A, const float *B, float *C,
                       const size_t n, const size_t m, const size_t k)
{
    size_t blocks_n = (n / BLOCK_SIZE) * BLOCK_SIZE;
    size_t blocks_k = (k / BLOCK_SIZE) * BLOCK_SIZE;
    for (i = 0; i < blocks_n; i += BLOCK_SIZE) {
	    for (j = 0; j < blocks_k; j += BLOCK_SIZE) {
	        process_block_4x4(m,
                              &A[i*m], m,
                              &B[j], k,
                              &C[(i*k) + j], k);
	    }
    }
}

Как мы будем реализовывать эту функцию? Для начала нужно загрузить блок матрицы C, в котором мы будем аккумулировать результат. Но перед использованием инструкции загрузки нам нужно сконфигурировать матричный регистр. В функции process_block4х4() мы, как и в скалярной версии, обрабатываем фиксированные блоки 4×4. Размер блока выбран не случайно. Это максимальный размер при ширине матричного регистра в 128 бит. Сконфигурируем эти блоки функциями mcfgm (), mcfgn () и mcfgk (). После конфигурации вызываем инструкцию загрузки этого блока mld_f32(), передавая указатель на матрицу С и страйд ldc * sizeof (float) — расстояние до следующей строки блока в байтах.

static inline void process_block_4x4(const size_t m,
                                     const float *A, const size_t lda,
                                     const float *B, const size_t ldb,
                                           float *C, const size_t ldc) {
    const size_t blocks_m = (m / BLOCK_SIZE) * BLOCK_SIZE;
 
    // Rows of matrix
    mcfgm(BLOCK_SIZE);
    // Rows of matrix B when multiplying
    mcfgn(BLOCK_SIZE);
    // Cols of matrix in bits
    mcfgk(BLOCK_SIZE * sizeof(float));
 
    // Load C (4 x 4) block
    mfloat32_t mc = mld_f32(C, ldc * sizeof(float));
 
    size_t block_m;
    for (block_m = 0; block_m < blocks_m; block_m += BLOCK_SIZE) { ... }
    ...
}

Следующие шаг после загрузки матрицы — реализовать цикл с загрузками блоков перемножаемых матриц и их умножением.

Реализуем цикл с загрузками блоков перемножаемых матриц и их умножением

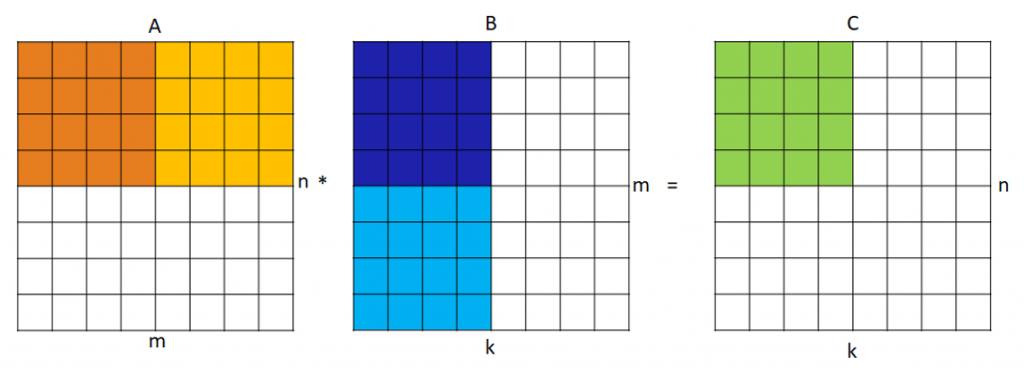
Для загрузки блока A мы просто вызываем инструкцию загрузки со страйдом lda * sizeof (float), который соответствует числу столбцов матрицы A. Матричный регистр переконфигурировать нам не нужно, потому что ранее мы уже сделали это для блоков 4×4. Для загрузки матрицы B, однако, нам сначала нужно ее транспонировать и загрузить в отдельный буфер 4×4. А уже после загрузить в матричный регистр инструкцией mld_f32(), со страйдом 4*sizeof (float).

Зачем нужно это транспонирование?

На первый взгляд, это рудиментарно. Мы делаем умножение матриц, зачем-то еще транспонируем — все это это лишние операции загрузки и сохранения. Дело в том, что этого требует спецификация. На GitHub в описании этой инструкции явно указано, что она умножает блок матрицы A на транспонированный блок матрицы B. Зачем это нужно, мы расскажем чуть позже, а пока просто подчинимся этому требованию: сказали транспонировать — нужно транспонировать.

После загрузки блоков мы можем умножать их с помощью инструкции fmmacc_mf32().

Опять же, реконфигурация матричного регистра нам не требуется, все уже сконфигурировано до размера 4. После того, как мы умножили, продвигаем наши указатели: указатель ptr_a на 4, потому что мы двигаемся слева направо, a указатель ptr_b мы передвигаем на ldb*4, так как двигаемся сверху вниз.

 ...
    const float *ptr_a = A;
    const float *ptr_b = B;
 
    float block_b[BLOCK_SIZE * BLOCK_SIZE];
    const size_t stride_a = lda * sizeof(float);
 
    size_t block_m;
    for (block_m = 0; block_m < blocks_m; block_m += BLOCK_SIZE) {
	    // Load A (4 x 4) block
	    mfloat32_t ma = mld_f32(ptr_a, stride_a);
 
	    // Transpose B (4 x 4) block
	    for (int row = 0; row < BLOCK_SIZE; row++) {
	        for (int col = 0; col < BLOCK_SIZE; col++) {
	            block_b[col*BLOCK_SIZE+row] = ptr_b[(row * ldb) + col];
	        }
	    }
 
	    // Load B (4 x 4) block
	    mfloat32_t mb = mld_f32(block_b, BLOCK_SIZE * sizeof(float));
 
	    // C (4 x 4) += A (4 x 4) * B (4 x 4) ^ T
	    mc = fmmacc_mf32(mc, ma, mb);
 
        ptr_a += BLOCK_SIZE;
        ptr_b += BLOCK_SIZE * ldb;
    }
 
    // Store C (4 x 4) block
    mst_f32_mf32(C, ldc * sizeof(float), mc);
}

Когда мы уже вышли из цикла и перемножили все блоки, мы должны сохранить блок матрицы C, в котором аккумулировали произведения блоков A и блоков B. Выполняется это так же, как и загрузка, только инструкцией сохранения mst_f32_mf32().

Умножение матриц произвольного размера

Но как быть, если размерности матриц не кратны 4? Например, длина строки A или столбца B не кратна 4, что не соответствует описанному выше алгоритму.

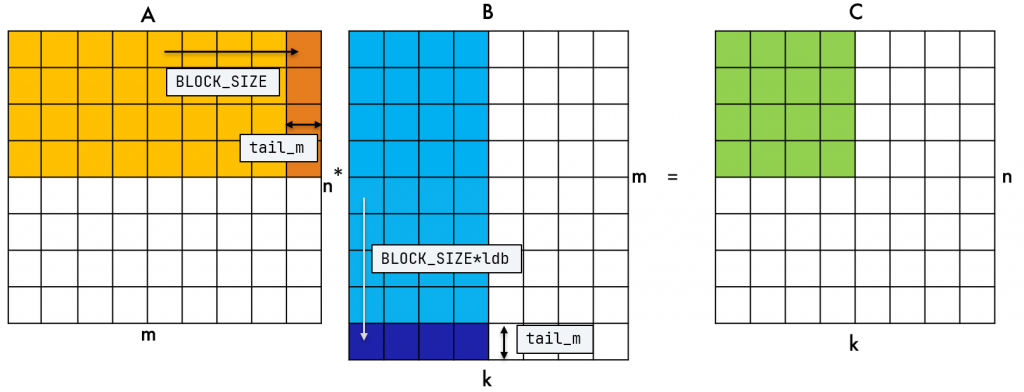
Введем новую переменную tail_m, обозначающую длину «хвоста» нашего скалярного произведения, который мы должны считать отдельно. Для этого мы сделаем одно ветвление и, если этот «хвост» существует, будем загружать также эти блоки меньших размеров.

Для загрузки матрицы A необходимо переконфигурировать только количество столбцов в байтах, равное tail_m * sizeof (float), так как у нас все еще 4 строки, но количество столбцов может быть от 1 до 3. Для матрицы B все аналогично тому, как это сделано в основном цикле — за исключением изменения одной размерности блока. Копируем блок tail_m x 4 с транспонированием во временный буфер, получается блок 4 x tail_m. Переконфигурировать матричный регистр не нужно, так как размерность совпадает с блоком матрицы А.

Теперь мы должны перемножить два загруженных блока. Переконфигурировать матричный регистр не нужно, потому что количество столбцов мы указали на предыдущем шаге, а все остальное мы сконфигурировали заранее, блок C у нас 4×4.

 const size_t blocks_m = (m / BLOCK_SIZE) * BLOCK_SIZE;
    const size_t tail_m = m - blocks_m;
    ...
    for (block_m = 0; block_m < blocks_m; block_m += BLOCK_SIZE) { ... }
 
    if (tail_m) {
        mcfgk(tail_m * sizeof(float));
	    // Load A (4 x tail_m) block
	    mfloat32_t ma = mld_f32(ptr_a, stride_a);
 
	    // Transpose B (tail_m x 4) block
	    for (int row = 0; row < tail_m; row++) {
	        for (int col = 0; col < k; col++) {
	            block_b[col*BLOCK_SIZE+row] = ptr_b[(row * ldb) + col];
	        }
	    }
 
	    // Load B (4 x tail_m) block
	    mfloat32_t mb = mld_f32(block_b, BLOCK_SIZE * sizeof(float));
 
	    // C (4 x 4) += A (4 x tail_m) * B (4 x tail_m) ^ T
	    mc = fmmacc_mf32(mc, ma, mb);
    }
 
    mcfgk(BLOCK_SIZE * sizeof(float));
    // Store C (4 x 4) block
    mst_f32_mf32(C, ldc * sizeof(float), mc);
}

После этого нужно слегка изменить сохранение блока матрицы C. А именно — переконфигурировать размер блока C для сохранения, так как при обработке хвоста размерность была изменена.

Но на этом наша работа не окончена, потому что у нас три размерности, а не одна, и размерности N или K могут быть не кратны 4. Нужно учитывать случаи, когда в обрабатываемом блоке матрицы C или количество столбцов, или количество строк, или количество и строк, и колонок меньше четырех.

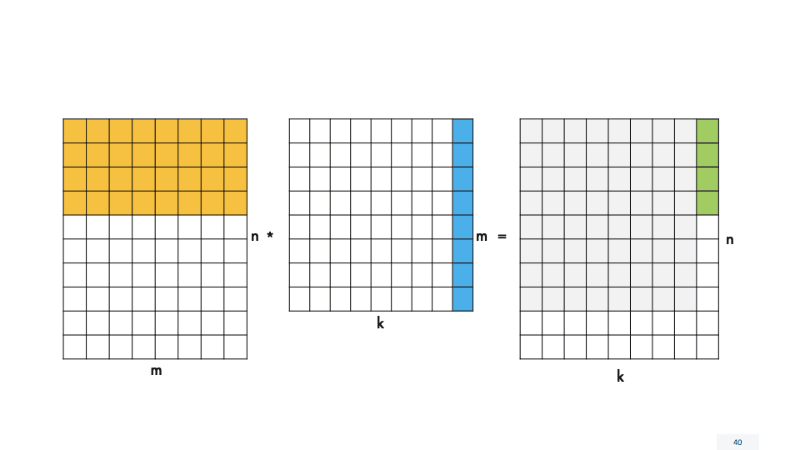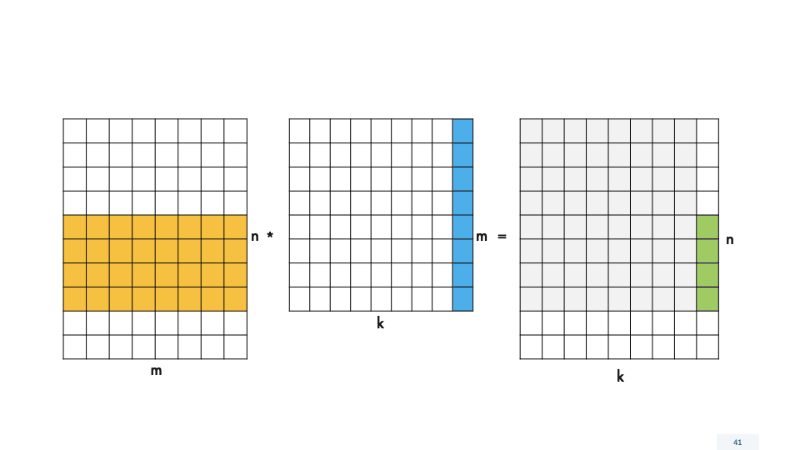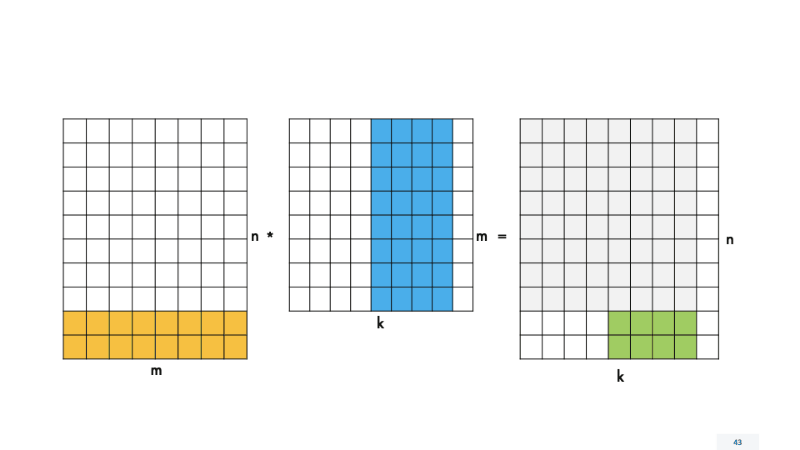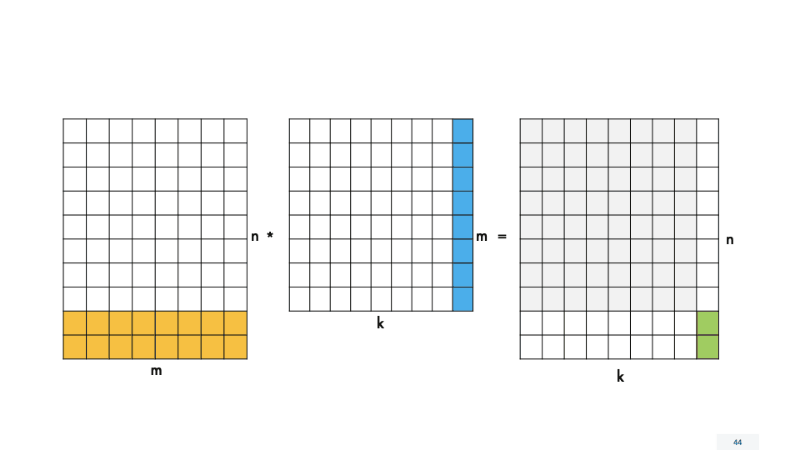
Для этого изменим функцию process_block₄×4(), в которой происходит расчет скалярных произведений. Теперь она будет называться process_block_nxk () и работать с любым количеством строк и столбцов в блоке. Для размера блока 4×4, который мы рассмотрели ранее, ничего не поменяется. Мы будем передавать в функцию размер 4×4, и все будет работать, как раньше. Но нам нужно обрабатывать «хвосты» по N и K, поэтому для наглядности разделим вызовы функций на четыре случая с разным размером блоков.

void gemm_block4x4_rvm(const float *A, const float *B, float *C, const size_t n, const size_t m, const size_t k)
{
    size_t blocks_n = (n / BLOCK_SIZE) * BLOCK_SIZE;
    size_t blocks_k = (k / BLOCK_SIZE) * BLOCK_SIZE;
 
    size_t tail_n = n - blocks_n;
    size_t tail_k = k - blocks_k;
 
    size_t i;
    size_t j;
    for (i = 0; i < blocks_n; i += BLOCK_SIZE) {
        for (j = 0; j < blocks_k; j += BLOCK_SIZE) {
            process_block_nxk(BLOCK_SIZE, BLOCK_SIZE, m, &A[i*m], m, &B[j], k, &C[(i*k) + j], k);
        }
        if (tail_k != 0) {
            process_block_nxk(BLOCK_SIZE, tail_k, m, &A[i*m], m, &B[j], k, &C[(i*k) + j], k);
        }
    }
    if (tail_n != 0) {
        for (j = 0; j < blocks_k; j += BLOCK_SIZE) {
            process_block_nxk(tail_n, BLOCK_SIZE, m, &A[i*m], m, &B[j], k, &C[(i*k) + j], k);
        }
        if (tail_k != 0){
            process_block_nxk(tail_n, tail_k, m, &A[i*m], m, &B[j], k, &C[(i*k) + j], k);
        }
    }
}

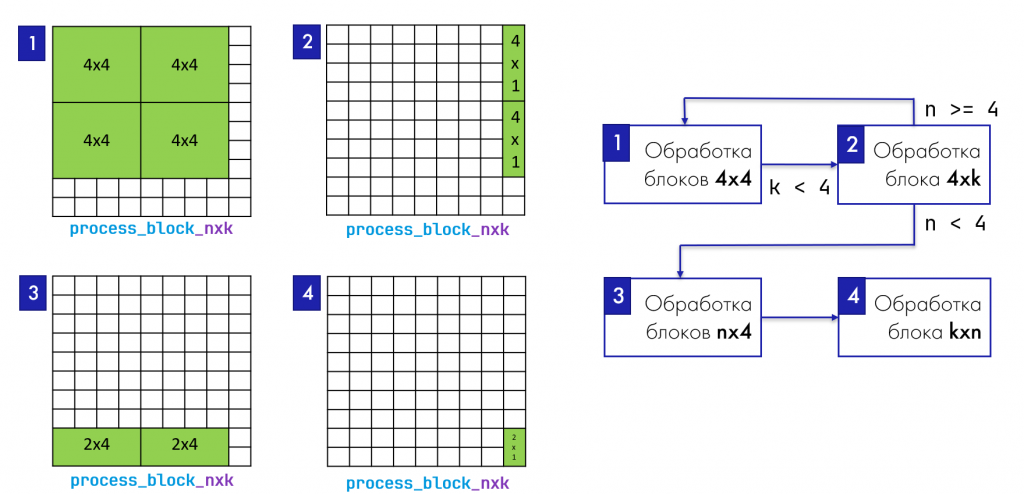
Четыре случая с разными размерами блоков

Теперь нужно изменить реализацию функции вычисления process_block_nxk () для работы с различными размерами блоков. Она будет очень схожа с прошлой версией функции, только мы будем по-другому конфигурировать матричный регистр. Рассмотрим на примере самого последнего случая — блока kxn, потому что, если мы реализуем функцию для него, реализуем и для остальных случаев.

Сконфигурируем матричный регистр по размеру блока C, который, как раньше, сначала нужно загрузить.

static inline void process_block_nxk(const size_t n, const size_t k, const size_t m,
                                     const float *A, const size_t lda,
                                     const float *B, const size_t ldb,
                                           float *C, const size_t ldc) {
    const size_t blocks_m = (m / BLOCK_SIZE) * BLOCK_SIZE;
 
    mcfgm(n);
    mcfgk(k * sizeof(float));
    // Load C (n x k) block
    mfloat32_t mc = mld_f32(C, ldc * sizeof(float));
 
    size_t block_m;
    for (block_m = 0; block_m < blocks_m; block_m += BLOCK_SIZE) { ... }
 
    if (tail_m) { ... }
 
    // Store C (n x k) block
    ...
}

Дальше идет основной цикл перемножения блоков, где мы пока еще не дошли до «хвоста». То есть количество столбцов у матрицы A в этом цикле у нас 4, количество строк уже может меняться в зависимости от размера блока. Перед загрузкой блока матрицы A нам нужно сконфигурировать матричный регистр на размер Nх4. С матрицей B то же самое: мы ее транспонируем и копируем во временный буфер. Конфигурируем только одну размерность, так как блок размерности Kх4, и загружаем.

После загрузки — умножение двух загруженных блоков, для которых нужно соответствующим образом переконфигурировать матричный регистр относительно блока матрицы C размера NxK, который мы хотим рассчитать. Количество столбцов матриц A и B мы сконфигурировали при загрузке блоков A и B, оно у нас остается.

...
    for (block_m = 0; block_m < blocks_m; block_m += BLOCK_SIZE) {
	    mcfgm(n);
	    mcfgk(BLOCK_SIZE * sizeof(float));
	    // Load A (n x 4) block
	    mfloat32_t ma = mld_f32(ptr_a, stride_a);
 
	    // Transpose B (4 x k) block
	    for (int row = 0; row < BLOCK_SIZE; row++) {
	        for (int col = 0; col < k; col++) {
	            block_b[col*BLOCK_SIZE+row] = ptr_b[(row * ldb) + col];
	        }
	    }
	    mcfgm(k);
	    // Load B (k x 4) block
	    mfloat32_t mb = mld_f32(block_b, BLOCK_SIZE * sizeof(float));
 
	    mcfgm(n);
	    mcfgn(k);
	    // C (n x k) += A (n x 4) * B (k x 4) ^ T
	    mc = fmmacc_mf32(mc, ma, mb);
 
        ptr_a += BLOCK_SIZE;
        ptr_b += BLOCK_SIZE * ldb;
    }
    if (tail_m) { ... }
    ...
}

После перемножения блоков в основном цикле идет обработка «хвоста» — обрабатываются самые маленькие блоки. Для блока матрицы A количество строк остается также N, но количество столбцов теперь не фиксированное 4, а tail_m, то есть наш «хвост». Для матрицы B все то же самое. Количество столбцов в блоке после транспонирования теперь tail_m, а не 4.

Далее умножение блоков. Количество столбцов матрицы A и матрицы B сконфигурированы при загрузке блоков, а количество строк и столбцов матрицы C необходимо переконфигурировать. Перемножив блоки, конфигурируем размерность матричного регистра на размер столбцов блока С. Раньше она была равной tail_m, теперь должна быть k. Сохраняем блок матрицы C.

 ...
    for (block_m = 0; block_m < blocks_m; block_m += BLOCK_SIZE) { ... }
 
    if (tail_m) {
	    mcfgm(n);
	    mcfgk(tail_m * sizeof(float));
	    // Load A (n x tail_m) block
	    mfloat32_t ma = mld_f32(ptr_a, stride_a);
 
	    // Transpose B (tail_m x k) block
	    for (int row = 0; row < tail_m; row++) {
	        for (int col = 0; col < k; col++) {
	            block_b[col*BLOCK_SIZE+row] = ptr_b[(row * ldb) + col];
	        }
	    }
 
	    mcfgm(k);
	    // Load B (k x tail_m) block
	    mfloat32_t mb = mld_f32(block_b, BLOCK_SIZE * sizeof(float));
 
        mcfgm(n);
	    mcfgn(k);
	    // C (n x k) += A (n x tail_m) * B (k x tail_m) ^ T
	    mc = fmmacc_mf32(mc, ma, mb);
    }
 
    mcfgk(k * sizeof(float));
    // Store C (n x k) block
    mst_f32_mf32(C, ldc * sizeof(float), mc);
}

Следующие шаги в оптимизации

Можно сказать, что на этом реализация матричного умножения с помощью матричного расширения T-Head для матриц произвольного размера завершена. Но будет ли это работать быстро? Пока не запустим эту реализацию на реальном железе, мы не узнаем. Но оптимизация умножения матриц — это не только использование векторных или матричных инструкций, но и оптимизация доступов к памяти.

В предыдущих статьях серии про матричные расширения Валерия не раз упоминала работу Goto и Geijn. Основная идея этой статьи — многоуровневое блокирование относительно кэшей и переупорядочивание элементов. Что же это значит?

Не секрет, что процессор имеет многоуровневую иерархию памяти. Самая быстрая память — регистры, но их меньше всего. Далее идет L1-кэш, потом L2, L3 и оперативная память. Сейчас наша реализация не использует эффективно ни регистры, ни кэши процессора. Если с регистрами понятно — нужно увеличить размер блока и использовать все 8 регистров (сейчас мы используем 3), то как быть с кэшами?

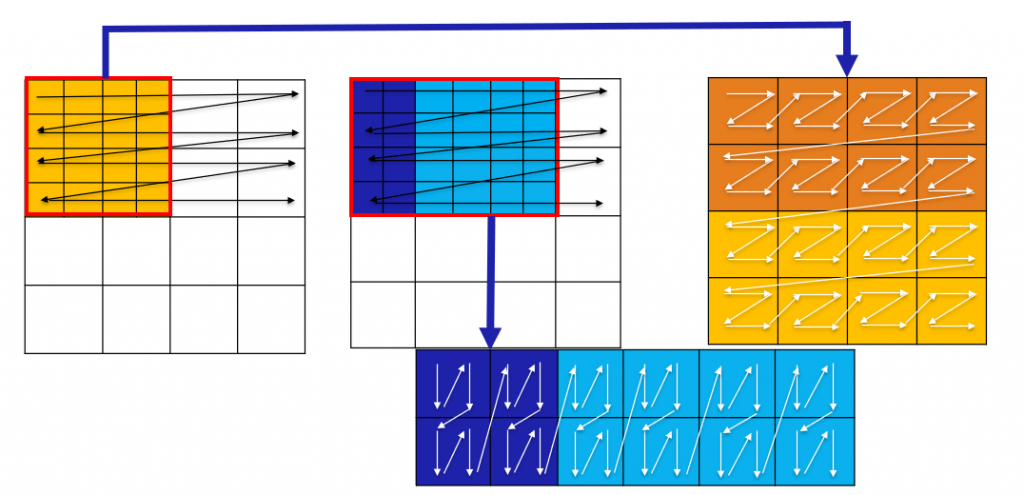
Идея в том, чтобы нарезать матрицы A и B на большие блоки, пока они влезают в кэши. На изображении ниже мы выделяем большой блок матрицы B такого размера, чтобы он полностью влезал в L3-кэш. Дальше берем блок матрицы A поменьше, чтобы он влезал в L2-кэш. После этого возвращаемся к матрице B и выделяем подблок в L3, который помещался бы в L1-кэш. Таким образом, мы будем максимально утилизировать иерархию кэшей и уменьшим задержку загрузок элементов матрицы в регистры.

Но как определить размеры этих блоков? Они зависят от размеров кэшей на конкретном процессоре и типа данных матрицы.

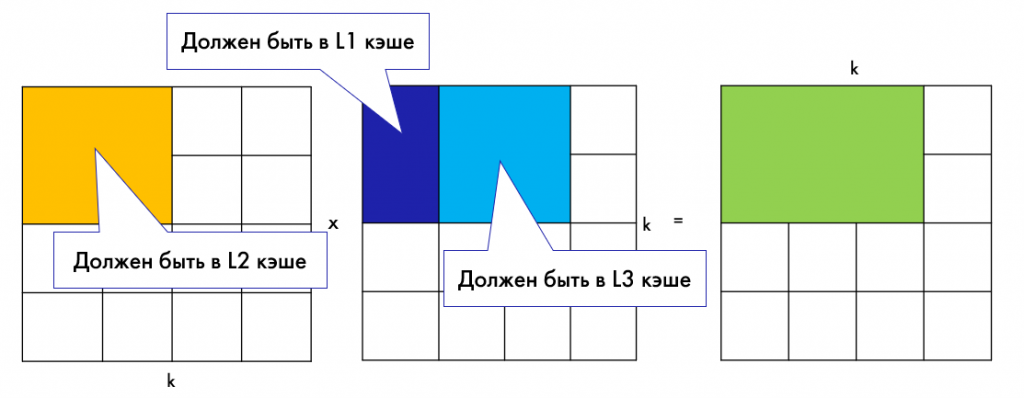
Распределение блоков матриц по разным уровням кэша

Как действовать дальше? Перемножить два блока A из L2 и B из L1 и перейти к блоку матрицы B, который правее и лежит в L3. После того, как умножили весь блок B из L3, загрузить новые блоки. А уже внутри этих блоков использовать реализованное нами умножение блоками 4×4 (или больше, если использовать все регистры матричного расширения).

Но это не решает проблему с доступами к элементам матрицы внутри блока. Они лежат в кэше, но перед загрузкой в матричный регистр нам нужно транспонировать блок матрицы B. Тут на помощь приходит переупорядочивание. Копируя большой блок матрицы В, который должен умещаться в кэше, заодно можно расположить элементы так, чтобы при загрузке в регистр они лежали в памяти последовательно. Иначе говоря, leading dimension равен количеству колонок матрицы. Также нужно не забывать про транспонирование матрицы B.

Помимо упомянутой статьи Goto и Geijn, в интернете есть множество материалов про оптимизацию умножения матриц. Если вы не хотите погружаться в большие научные работы, могу посоветовать две статьи с пошаговой оптимизацией умножения матриц:

The GotoBLAS/BLIS Approach to Optimizing Matrix-Matrix Multiplication — Step-by-Step Роберта ван де Гейна.
Умножение матриц: эффективная реализация шаг за шагом — отличная статья с кодом, комментариями и иллюстрациями на Хабре.

Наверх

4 комментария

Сергей
4 месяца назад

Зачем вообще говорить о некратной 4 матрице?
- Валерия Пузикова
  4 месяца назад
  
  В реальных задачах матрицы произвольного размера и не обязаны быть кратными 4-м. Поэтому рассматривается общий случай.
Игорь
2 месяца назад

Собаку съел в своё время на LAPACK, BLAS и их производных (хоздоговора, диссертация и т. п.). Не нашёл в статье ни слова про проблему потери значимости при матричном умножении с плавающей точкой (писали люди, для которых численные алгоритмы -- не главное?). Без решения этой проблемы ни о какой реализации в железе не может идти и речи, это будет полный провал.
- admin
  2 месяца назад
  
  Здравствуйте, Игорь! Операция матричного умножении основана на скалярном произведении, которое вычисляется в соответствии с IEEE-754 (указано в спецификации расширения).
  В статье не уделяется этому внимания, так как она призвана показать основные идеи матричного расширения от компании T-Head на примере матричного умножения.