Не так-то просто вспомнить законченное электронное устройство, которое обходится без такой важной детали, как резистор. Поэтому мы стартуем изучение электроники в курсе по схемотехнике для начинающих именно с него.
Само название «резистор» происходит от латинского resisto — сопротивляюсь. Чему же он сопротивляется? Чтобы разобраться, нужно вспомнить школьный курс физики. В этом материале мы разберемся с основами физики тока: напряжением, силой тока, тем самым сопротивлением и мощностью. Мы не будем полностью повторять главы учебников по этим темам, а напомним только самые главные определения, чтобы автор и читатели были на одной волне. Также для легкости понимания принципов мы будем упрощать некоторые сложные явления, чтобы не утонуть в обилии подробностей.
Электрическое напряжение
Все объекты вокруг нас состоят из атомов. А они, в свою очередь, — из положительно заряженных ядер и движущихся вокруг них отрицательно заряженных электронов. Знаки зарядов были назначены физиками для удобства, на самих ядрах и электронах ничего такого не написано.
Мы можем каким-либо способом — химическим или механическим — разделить положительные и отрицательные заряды. Например, за счет трения сорвать часть электронов с атомов и заставить их скопиться в одной области. Пострадавшие же от этого «грабежа» атомы останутся в другой части.
Такое разделение зарядов называется электризацией, наблюдать его можно, например, во время расчесывания волос. Часто при этом можно заметить, как волоски начинают тянуться вслед за расческой. Из-за трения на расческе и волосах образуются разноименные заряды, которые притягиваются друг к другу с целью вернуть «украденные» электроны обратно в свои атомы и восстановить утраченное равновесие. А вот одноименные заряды, наоборот, отталкиваются, ведь при их взаимодействии равновесие не восстановится.
Физики при этом говорят, что между разделенными зарядами возникает электрическое поле, направленное от положительных зарядов к отрицательным. Направление условились считать таким для определенности.
Чтобы определить силу взаимодействия электрических зарядов друг с другом и совершаемую электрическим полем работу при перемещении зарядов, ввели понятие разности потенциалов или напряжения между точками в электрическом поле.
На практических занятиях курса мы с вами будем проводить несложные расчеты, чтобы вы научились самостоятельно собирать разные электрические схемы. Для этого нужно познакомиться с несколькими определениями и формулами — обойтись без них не получится, поскольку это основы основ всей электроники.
Величину заряда, о которой мы говорили выше, измеряют в кулонах. Кулоны показывают количество электричества, как бы странно это ни звучало. На текущий момент элементарным зарядом, то есть таким, меньше которого быть не может, является заряд электрона. Он очень мал, один кулон равен заряду вместе взятых 6 241 509 074 460 762 608 электронов! А единицей измерения работы, которую совершают силы электрического поля для перемещения таких зарядов, являются джоули. Зная об этом, мы можем определить для себя напряжение.
Поясним это определение с помощью рисунка, взятого из «Элементарного учебника физики» под редакцией академика Ландсберга. Многие преподаватели до сих пор считают его лучшим учебником для школьников за подробные и доходчивые объяснения по всем темам, хотя эта книга и не входит в образовательную программу.
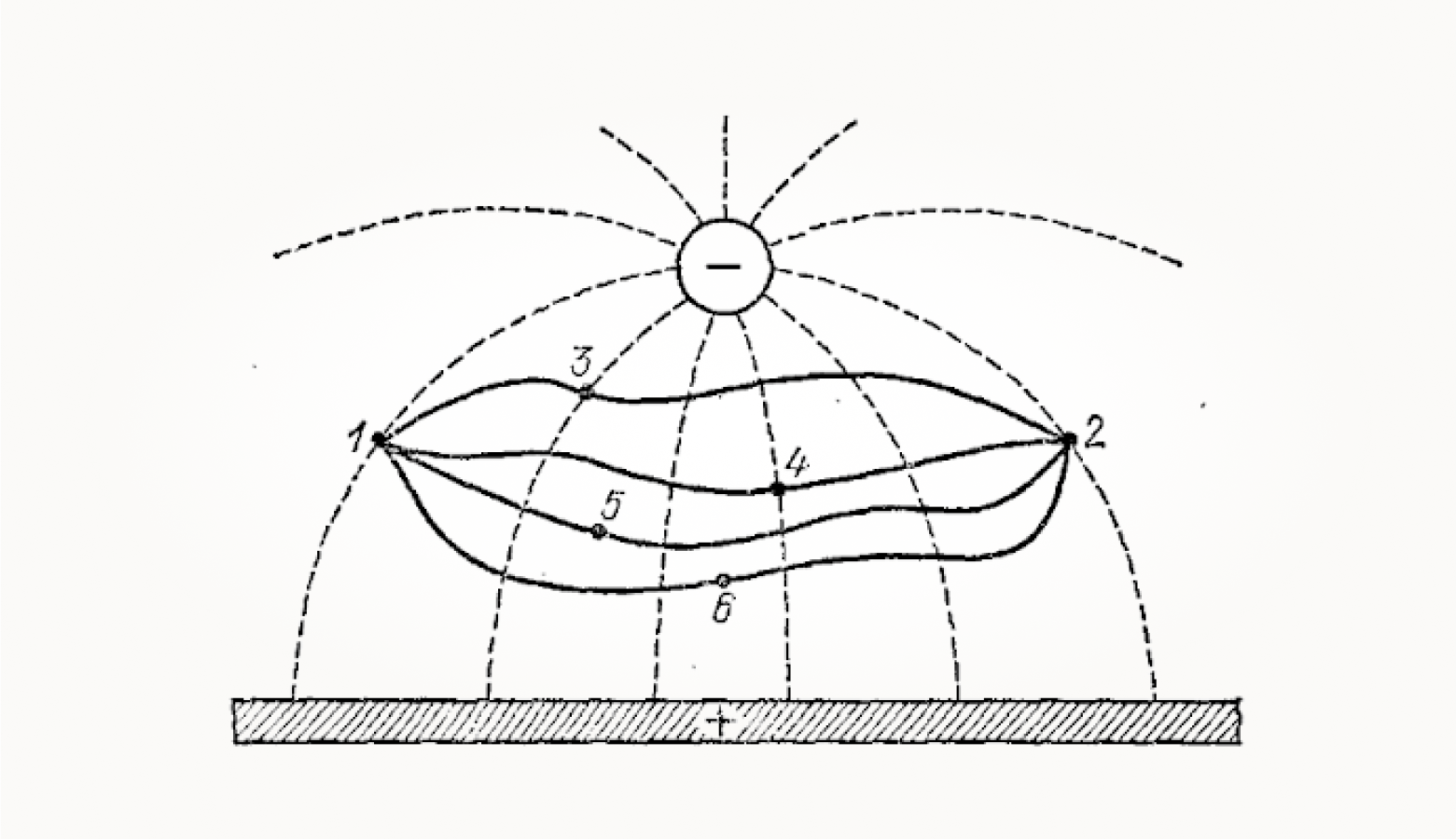
На рисунке есть шарообразный отрицательный заряд, который взаимодействует с положительно заряженной плоскостью. Пунктиром обозначены силовые линии электрического поля между этими двумя заряженными объектами. Эти воображаемые линии в пространстве показывают, как будет направлено движение свободной заряженной частицы, оказавшейся в зоне действия данного электрического поля. Электрическая сила, действующая на такую частицу, будет направлена по касательной к силовой линии в том месте, где сейчас находится частица. И в зависимости от знака своего заряда частица полетит либо к плоскости, либо к шару.
Теперь предположим, что у нас есть возможность каким-то образом воздействовать на движение заряженной частицы в электрическом поле. Заставим ее переместиться из точки 1 в точку 2 по любой из четырех траекторий, проходящих через точки 3, 4, 5, 6. Если какой-то участок траектории направлен в ту же сторону, куда стремилась бы сама заряженная частица, то электрическое поле будет нам помогать в ее перемещении. А в обратном случае — препятствовать.
Это значит, что на разных участках нам потребуется совершить разную работу, чтобы заставить частицу двигаться туда, куда нам нужно, а не куда ей хочется. Можно строго математически доказать (и в учебнике Ландсберга это проделано), что итоговая работа по перемещению частицы из точки 1 в точку 2 совершенно не зависит от траектории движения. Она зависит только от положения начальной и конечной точек в электрическом поле.
Получается, что при известной величине заряда частицы, работа по ее перемещению из точки 1 в точку 2 может служить количественной характеристикой электрического поля. Если поле «сильнее», то нам потребуется совершить над частицей одну работу, а если «слабее», то другую. Именно величина этой работы и получила название разности потенциалов или напряжения, как было написано в определении выше.
Работа в электрическом поле может быть:
- положительной, когда она совершается в том направлении, куда «тащит» частицу электрическое поле,
- отрицательной, когда нам приходится тянуть частицу против поля.
Поэтому и напряжение может быть и положительным, и отрицательным, что и происходит на практике, когда мы измеряем его приборами.
Иногда ошибочно говорят про потенциал в какой-то точке электрического поля. Физический смысл имеет только разность потенциалов, так как абсолютного нуля для отсчета потенциала не существует. Как не существует и абсолютного нуля при отсчете высот на Земле: мы считаем от уровня моря, а никто не мешает делать это от вершины Эвереста, от дна Марианской впадины или от центра Земли — это все вопрос договоренностей. Так же и с электрическим потенциалом: что считать за ноль — вопрос предпочтений. По этой причине нас будет интересовать только напряжение, разность потенциалов, а за ноль мы во всех дальнейших материалах будем принимать минусовой вывод батарейки питания.
В батарейках заряды разделяются химическим способом при производстве. Между двумя полюсами батарейки, которые называют электродами, существует электрическое напряжение. Его величина указана на корпусе.
Например, для обычной «пальчиковой» батарейки это 1.5 В, а для батареек типа «Крона», которые мы будем использовать в своих экспериментах, — 9 В.
Дома можно за пару минут создать на кухонном столе батарейку из картошки, лимона или какого-нибудь другого плода. Для этого нужно воткнуть него два электрода: медный гвоздь или проволоку и оцинкованный гвоздь. Цинк будет отдавать электроны, медь — принимать, а сок плода выполнит роль электролита, переносящего заряд.
Прибор для измерения напряжения — вольтметр — может показать вполне приличное напряжение между электродами «лимонной» батарейки. Особенно если несколько таких элементов питания соединить проводами друг за другом в гирлянду, поочередно подключая медные электроды к цинковым. Подробнее о том, как это сделать, вы узнаете из второго ролика курса.
Только вот заставить работать от «лимонной» батарейки что-то серьезное не получится, максимум удастся получить тусклый свет от светодиодного фонарика. То есть одного напряжения в батарейке для хорошего питания электроники мало, нужно учесть что-то еще, необходимое для работы устройств. Мы еще вернемся к этому вопросу.
Сила тока и сопротивление
Чтобы заряд перемещался из одной точки в другую, необходимо создать для него путь, по которому он сможет бежать легко. Один из вариантов: просто прокинуть провод между областями с разноименными зарядами. Все провода делают из проводников. Это вещества, в которых электроны могут перемещаться легко и непринужденно, например, металлы. Как только заряды целеустремленно куда-то ринутся, возникнет не хаотичное, а направленное движение электрических частиц, которое и называется электрическим током.
Сила тока измеряется в амперах. Чтобы разобраться с ее определением, нам нужно ввести новый термин — поперечное сечение. Если положить огурец на доску и разрезать его поперек под прямым углом, то получится срез в виде круга, который и называют поперечным сечением. С проводом все то же самое, просто там круг будет иметь меньшую площадь.
На заре изучения электрических явлений физики не знали, что переносчиками заряда в проводниках служат отрицательно заряженные электроны, поэтому решили, что ток направлен от плюса к минусу. Потом, когда с электронами разобрались, менять уже ничего не стали. Так что и нам деваться некуда, будем тоже рисовать направление тока от плюса к минусу из уважения к традиции.
Если бы проводники были идеальными, то заряды летели бы по ним беспрепятственно. Однако ничего идеального в природе нет, поэтому внутри металлов электроны взаимодействуют с атомами их кристаллической решетки, замедляя от этого свой бег. Причем в разных веществах замедление имеет разную величину. А значит, его тоже надо измерить и охарактеризовать. Если взять куски разных проводников одной длины, одинакового поперечного сечения и в одних и тех же условиях приложить к их концам одинаковое напряжение, то сила тока в них будет разной.
Единица измерения названа в честь физика Георга Симона Ома, который сформулировал одноименный закон. Любой электронщик помнит закон Ома наизусть: «Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению». В виде формулы закон Ома записывается так:
где I — сила тока в проводнике, U — напряжение на концах проводника, а R — его сопротивление.
Итак, мы дали ответ на вопрос, заданный в начале текста. Резистор оказывает сопротивление току, протекающему через него, и ограничивает его до величины, зависящей от собственного сопротивления.
Заодно становится понятно, почему ранее описанная «лимонная» батарейка такая слабая: она не в силах отдать большой ток из-за наличия в ней заметного собственного внутреннего сопротивления. В хороших батарейках внутреннее сопротивление тоже есть, но оно достаточно мало. Правда, со временем электролит в батарейках может высохнуть: вольтметр покажет, что напряжение в норме, но от этой батарейки ничего не будет работать. Это происходит потому, что внутреннее сопротивление от пересыхания выросло, и здесь ничего не поделать.
Иногда физические величины слишком велики или слишком малы, и их значения становится неудобно писать из-за большого количества цифр. Тогда прибегают к известным греческим приставкам: 1 килоом = 1 кОм = 1000 Ом. 1 мегаом = 1 МОм = 1000000 Ом. Эти же приставки используются для упрощения записи токов и напряжений: килоампер, киловольт, мегаампер и мегавольт. Правда, это очень большие значения, поэтому чаще применяются уменьшающие приставки. Например, 1 миллиампер = 1 мА = 0,001 А, 1 микровольт = 1 мкВ = 0,000001 В.
Последовательное и параллельное соединение проводников
Из закона Ома вытекают два важных следствия про последовательное и параллельное соединение проводников. Если несколько резисторов соединены последовательно друг за другом, то через каждый из них течет один и тот же ток. Легко проверить, что это так. Как мы помним, ток определяется как заряд, протекающий через данную точку в электрической цепи в течение секунды.
Если токи в последовательной цепочке резисторов были бы разные, то это бы означало, что в каком-то из них накапливается электрический заряд. И мы смогли бы обнаружить это по воздействию на другой заряд, например, на любой наэлектризованный предмет. Однако физики выяснили, что на практике такого не происходит.
Когда мы перейдем к экспериментам, вы сможете при желании собрать последовательную цепочку из разнообразных резисторов и поднести к ним легкий наэлектризованный предмет. Для этих целей подойдет небольшой клочок тонкой бумаги или целлофановой упаковочной пленки. Чтобы предмет наэлектризовался, нужно потереть его об шерстную ткань — теплый свитер или зимний шарф. Наэлектризованный объект не будет притягиваться или отталкиваться от резисторов, через которые протекает ток, а с другими наэлектризованными предметами такое взаимодействие будет наблюдаться. Это и будет доказательством, что накопления зарядов в последовательной цепочке резисторов нет.
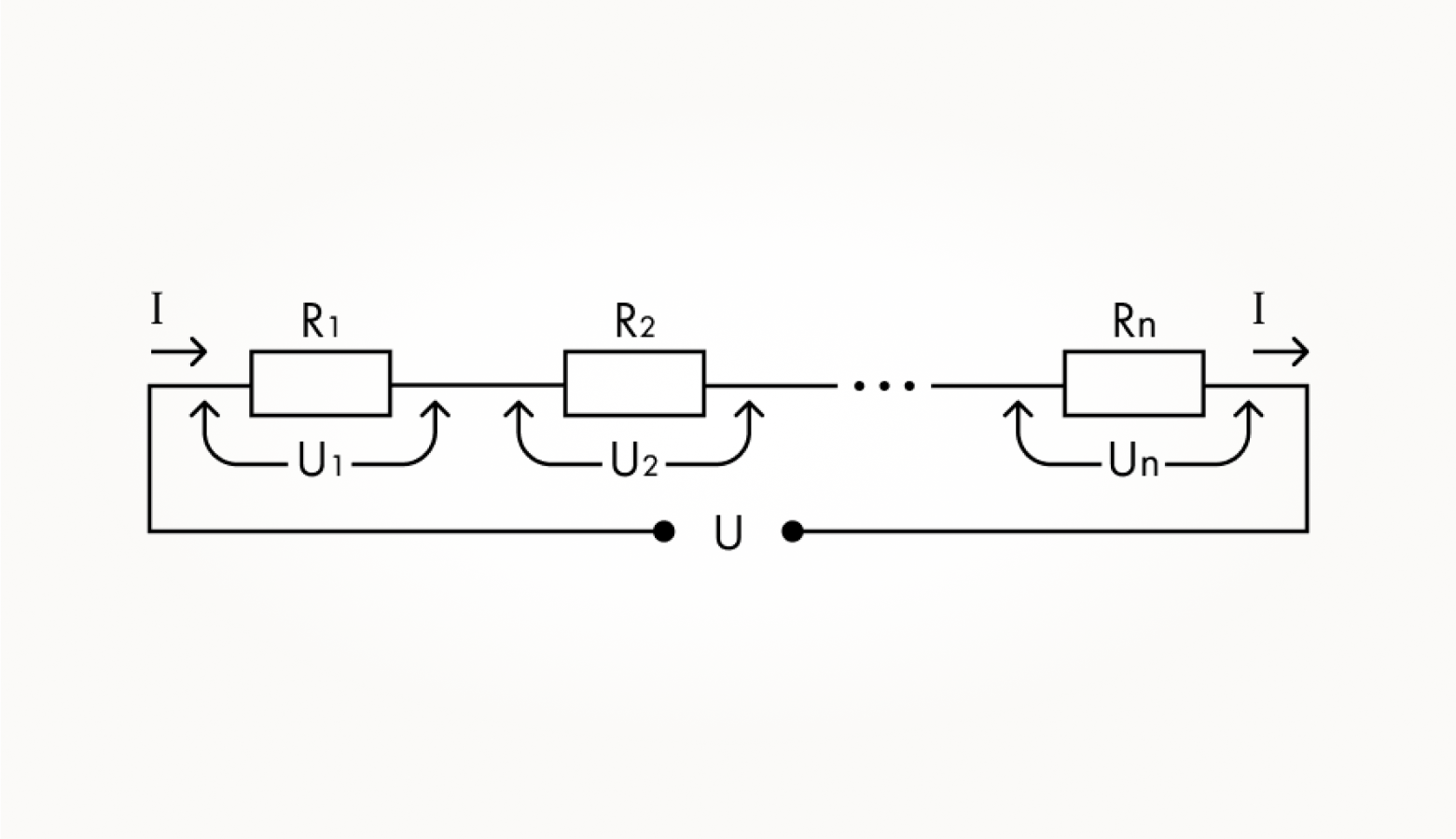
Итак, ток через все резисторы последовательной цепи одинаков и равен I. Напряжение на первом резисторе по закону Ома будет равно U1 = I x R1, на втором — U2 = I x R2, и так далее до Un = I x Rn. Напряжение U на концах всей цепи будет, конечно же, равно сумме напряжений на каждом из резисторов:
или
Выносим общий множитель за скобки:
И получаем по закону Ома, что общее сопротивление последовательной цепи равно сумме сопротивлений всех резисторов в цепи:
Если все резисторы одинаковые и сопротивление каждого равно R1, то формула упрощается до следующей:
А теперь рассмотрим цепочку параллельно включенных резисторов. На схеме не сразу бросается в глаза очень маленькая, но важная деталь. Речь о жирной точке на месте соединения пересекающихся проводов. Эту точку можно считать капелькой припоя, соединяющей такие проводники друг с другом и обеспечивающей контакт между ними. Если же на месте пересечения проводов на схеме точка не стоит, то это означает, что и контакта в этом месте нет. Просто было удобно провести линии на схеме так, будто один изолированный провод просто лежит на другом. После такого отступления можно изучить работу этой схемы.
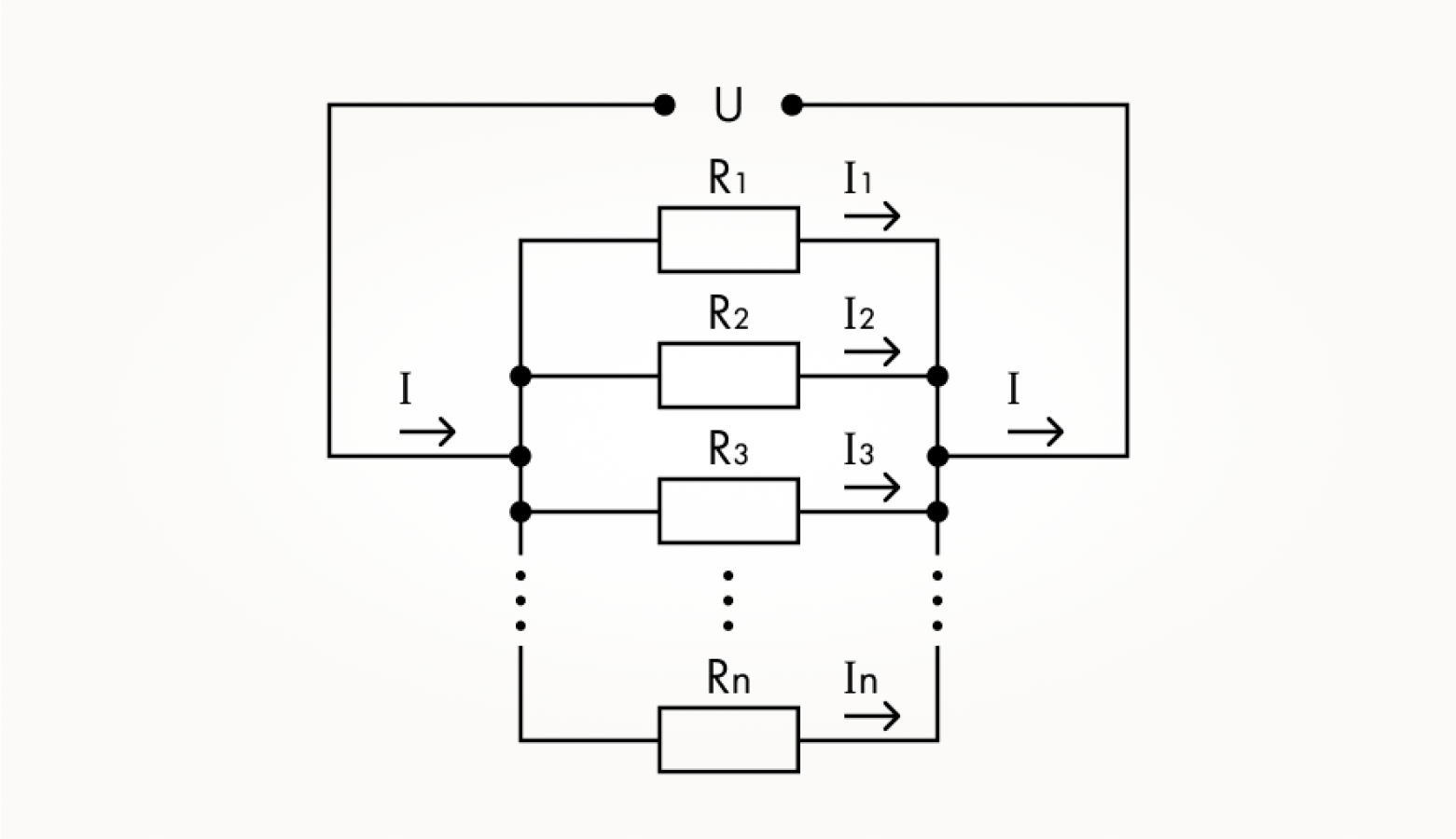
Ток в ней растекается по всем ветвям, а потом собирается обратно. Поэтому общая сила тока в цепи равна сумме токов через все резисторы:
Напряжение на всех резисторах в такой цепочке одинаково, иначе бы возникли токи, выравнивающие потенциалы в каждом узле схемы слева и справа, и они бы все равно неизбежно стали одинаковыми. Докажем это утверждение от противного, как говорят математики. Допустим, на левом конце резистора R1 потенциал стал по каким-то причинам больше, чем на левом конце второго резистора R2. В таком случае через проводник, соединяющий этими резисторы и обладающий очень низким сопротивлением, из-за разности потенциалов побегут электроны от одного резистора к другому, и через какое-то время эта разность потенциалов станет равной нулю, что и требовалось доказать. Поэтому:
Ток через каждый из резисторов вычисляется по закону Ома:
Подставляем эти выражения в формулу общей силы тока:
Так как I = U / R, где R — общее сопротивление всей цепи, то, сокращая U в числителях, получаем следующее выражение:
Величина 1/R, обратная сопротивлению, называется проводимостью и измеряется в Ом-1 или в сименсах (См) в честь другого немецкого ученого. Таким образом, закон Ома для параллельного соединения резисторов говорит, что проводимость такой цепи равна сумме проводимостей всех ее ветвей. Формула не такая удобная, как для последовательного соединения, но тут уж ничего не поделать.
Правда, жизнь становится чуть легче, если у нас все сопротивления одинаковы и равны R1:
Или если у нас сопротивления разные, но их всего два:
Внимательный читатель мог заметить, что при последовательном соединении резисторов общее сопротивление всегда больше любого, даже самого большого, сопротивления в этой цепочке. А в параллельной — меньше наименьшего. Если у вас при числовых расчетах получится не так, ищите ошибку, она точно где-то есть!
Электрическая мощность
Последняя важная физическая величина, без которой невозможно обойтись при изучении и разработке электроники, — мощность. Два физика Джоуль и Ленц открыли закон, который назван в их честь законом Джоуля-Ленца. Количество теплоты, выделяемой электрическим током в проводнике, равно произведению квадрата силы тока на сопротивление проводника и на время, в течение которого проводились измерения.
Эта единица измерения названа в честь одного из первых изобретателей паровой машины — Джеймса Ватта. Он же, кстати, придумал и первую единицу для измерения мощности: лошадиную силу.
С помощью закона Ома сформулируем все три возможных варианта для вычисления мощности в зависимости от того, какие параметры электрической цепи нам известны:
Зачем, казалось бы, нам задумываться об электрической мощности? А хотя бы потому, что неверный ее учет способен сжечь компонент на плате. И кстати, мы обязательно планируем это сделать, возможно, даже неоднократно! Следите за выходом наших материалов и обязательно пытайтесь повторить это дома: все наши эксперименты безопасны.
Например, выпускаемые промышленностью постоянные резисторы рассчитаны на определенную мощность. Это 0,125 Вт, 0,25 Вт, 0,5 Вт, 1 Вт, 2 Вт и более мощные. Если через резистор потечет ток, вызывающий выделение на нем большей мощности чем та, на которую он рассчитан, то он попросту сгорит.
Проведем несложный расчет. В рамках курса мы будем пользоваться батарейкой типа «Крона», которая в свежем состоянии выдает напряжение 9 В. Если мы подключим между ее плюсом и минусом резистор, например, сопротивлением 100 Ом, то получим мощность 0,81 Вт. Это значит, что резисторы, рассчитанные на мощность менее 1 Вт, будут сильно греться и даже сгорят! Поэтому расчет компонентов цепей на рассеиваемую в них мощность так важен. В наших экспериментах все предлагаемые схемы заранее рассчитаны таким образом, что в них всегда будет достаточно резисторов на мощность 0,25 Вт.
В инженерной среде можно часто услышать, как сопротивление резисторов называют словом «номинал».
Дело в том, что все электронные компоненты имеют некоторые отклонения от указанных в документации номинальных, то есть запланированных при изготовлении величин. Идеальное производство невозможно, всегда будут какие-то отклонения в технологическом процессе в ту или другую сторону.
Поэтому резистор с номинальным сопротивлением 1 кОм может в реальности иметь сопротивление 996 Ом или 1002 Ом. Все электронщики это знают, и никто не переживает по этому поводу. Мало где по-настоящему нужна высокая точность сопротивлений или других параметров у других компонентов. В наших будущих устройствах это точно так, они будут спокойно относиться к тому, что параметры немного «гуляют» туда-сюда.
Более того, если посмотреть на все номиналы наиболее массово выпускаемых резисторов, то окажется, что они имеют прерывистый ряд значений. Например, в интервале от 2 кОм до 3 кОм есть детали с сопротивлением 2 кОм, 2,2 кОм, 2,4 кОм, 2,7 кОм, но нет 2,5 кОм. Как же так? А никому не нужно подбирать сопротивление с высокой точностью в 90% случаев. Вычислили, скажем, что нужно сопротивление цепи 2,5 кОм, да и поставили туда любой резистор из двух ближайших в ряду номинальных сопротивлений.
Если все же точность требуется, то придется купить дорогие высокоточные резисторы, с отклонением от номинала на 0,1%, а не на 5−10%. Другой вариант — поставить в устройство подстроечный резистор, сопротивление которого плавно изменяется с помощью вращающейся ручки в заданном интервале сопротивлений. Подстроечные резисторы будут показаны в ролике по данной теме, а высокоточные постоянные нам не понадобятся.
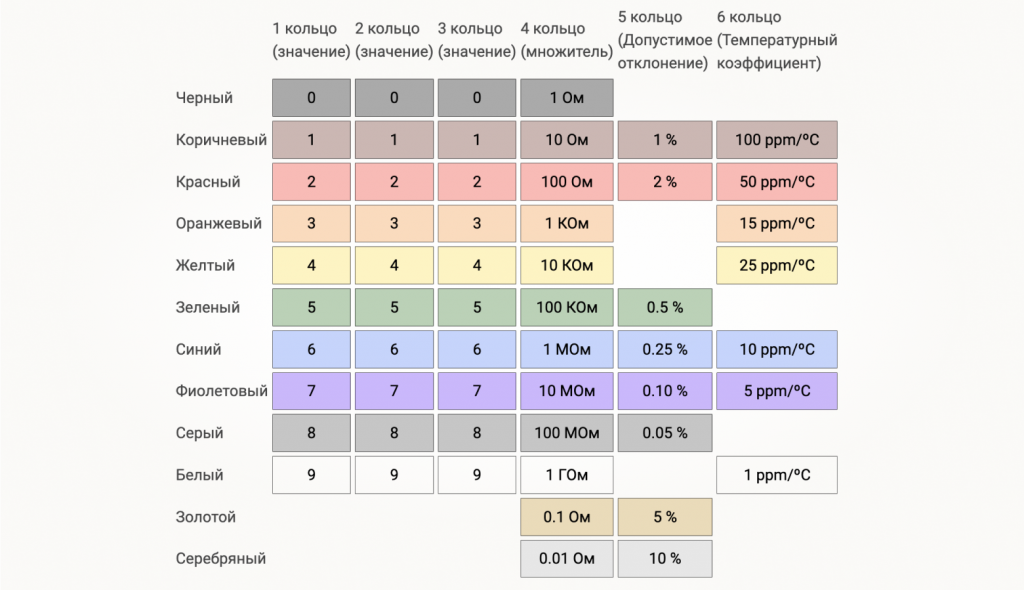
Номинальные сопротивления резисторов кодируются на корпусе разными способами. Например, текстом «1 кОм», но это встречается в основном на старых деталях или рассчитанных на большую мощность и поэтому крупных по размеру. Чаще на резисторах, которые мы будем устанавливать в макетную плату, маркировка выполняется цветными кольцами, где каждому цвету приписана определенная цифра.
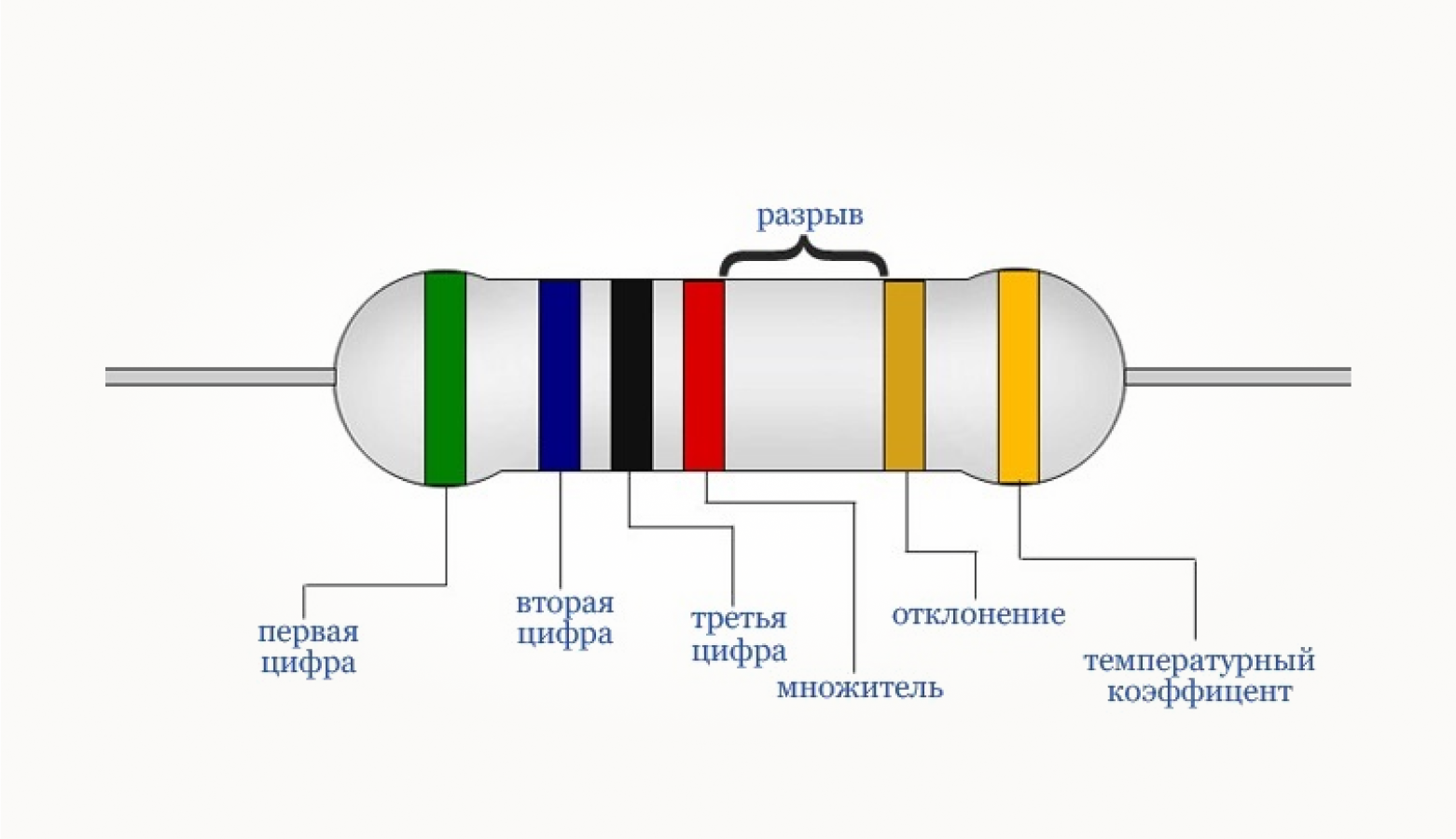
Первые три полосы, расположенные слева, обозначают величину сопротивления. Четвертая — это множитель, на которой нужно умножить число, полученное из предыдущих полос. Пятая полоса отображает отклонение величины сопротивления от номинального значения, а шестая, если она есть, нам неинтересна. При 4-полосной маркировке величина сопротивления кодируется только двумя левыми полосами. При 5- и 6-полосной маркировке в числе сопротивления используется три цифры.
Еще встречается маркировка только числами, как правило, на резисторах для поверхностного монтажа, которые нам в течение курса не пригодятся. Но знать об этом полезно. При трехзначной маркировке резисторов с сопротивлением свыше 10 Ом первые две цифры отражают начальное значение сопротивления, а последняя цифра — число нулей.
Если используется четырехзначная маркировка, то первые три цифры отражают начальное значение, а последняя цифра — число нулей. Например, маркировка «4703» кодирует сопротивление 470 000 Ом = 470 кОм. Для резисторов с сопротивлением менее 10 Ом в качестве запятой используется символ R. Так, маркировка «4R7» кодирует сопротивление 4,7 Ом, а маркировка «R47» означает сопротивление 0,47 Ом. Обратите внимание, что при трехзначной маркировке допустимое отклонение от номинального значения может быть ±2%, ±5% или ±10%, а при четырехзначной маркировке допустимое отклонение составляет ±1%.
Очепякта:
1 микровольт = 1 мкВ = 0,1 В.
Вадим, огромное спасибо вам за внимательность! Автоматический типограф на сайте решил внести свои правки в текст. Вы абсолютно правы.
Опечатки:
1) Этот абзац повторяется 2 раза: На практических занятиях курса мы с вами будем проводить несложные расчеты, чтобы вы научились самостоятельно собирать разные электрические схемы. Для этого нужно познакомиться с несколькими определениями и формулами — обойтись без них не получится, поскольку это основы основ всей электроники.
2) В формуле для двух сопротивлений индексы одинаковые: Или если у нас сопротивления разные, но их всего два: …
Олег, спасибо за вашу внимательность! Поправили 🙂
Поясните пожалуйста про величину измерения заряда.
1 кулон = 6 241 509 074 460 762 608 электронов! Это величина измерения ОТРИЦАТЕЛЬНОГО заряда, получается.
А какова величина измерения положительного заряда чему ровна?
Добрый день! В кулонах измеряется величина заряда независимо от его знака. Можно считать, что это модуль величины заряда в математическом смысле. Поэтому и для положительных, и для отрицательных зарядов используется одна и та же единица измерений.
Также напомним, что для всех участников курса у нас существует чат поддержки, где можно задать любые вопросы, которые возникли при изучении материала.