Обзор подходов к проблеме шероховатости фольги при проектировании высокоскоростных плат

Среди вызовов в разработке высокоскоростных цифровых плат особого внимания заслуживают следующие:

• Электромагнитная совместимость (EMC, или Electromagnetic Сompatibility),
• Целостность питания (PI, или Power Integrity),
• Целостность сигналов (SI, или Signal Integrity).

Представим, что случай у нас относительно простой: все чипы и их решения по питанию хорошо изучены и отхарактеризованы, а для закрытия вопроса ЭМС достаточно следовать лучшим практикам и не делать тривиальных ошибок. Иными словами, «гигиенические» факторы нас пока что не беспокоят и фокусироваться мы будем на проблеме целостности сигналов. Чтобы остаться в формате небольшой статьи, придется сделать несколько важных допущений. А именно:

• Мы ограничимся только интерфейсом PCIe, так как на основании спецификации PCIe легко составить ограничения при проектировании топологии шины.
• Мы ограничимся только теми участками топологии, которые контролируем при проектировании печатной платы, то есть одним сегментом физического канала. Это допущение хочется сделать, чтобы оградить себя от таких вещей, как FFE/CTLE/DFE, кабелей и прочих интересных, но нерелевантных в контексте статьи нюансов.
• Мы не берем в рассмотрение температурные зависимости любых параметров и производственные допуски на них.
• Мы не рассматриваем проблему перекрестных помех.

Спецификация PCIe говорит, что в рамках процедур валидации приемника должен использоваться калибровочный канал с номинальной величиной SDD21, равной -36 дБ. Это означает, что при проведении калибровки лишь 0.025% сгенерированной передатчиком энергии доходит до приемника, при этом приемнику позволено ошибочно определить лишь один бит из триллиона:

BER \le \frac{1}{10^{12}}.

Приведенная величина SDD21 не является нормативной, но несмотря на это часто используется в системном дизайне как некий ориентир, дающий простое представление о допустимой совокупной длине тракта и степени затухания сигнала в тракте.

Стоит сказать, что в реальности SDD21 не является мерой именно затухания, так как часть энергии отразится обратно в порт 1, не дойдя до порта 2. Для характеристики отражений используется величина SDD11, однако и она не характеризует одни лишь отражения, поскольку отраженная волна претерпевает затухания. Тем не менее, чтобы исключить эту сложность из нашей картины, будем считать, что величина SDD11 предельно мала в абсолютном выражении и что величина SDD21 обусловлена исключительно затуханиями в тракте.

Теперь проведем декомпозицию SDD21 с учетом всех принятых ранее допущений. Для этого возьмем абстрактную геометрию дифференциальной пары в абстрактном стеке и модель шероховатости, которую используемый софт предлагает по умолчанию. На выходе получаем следующую картину:

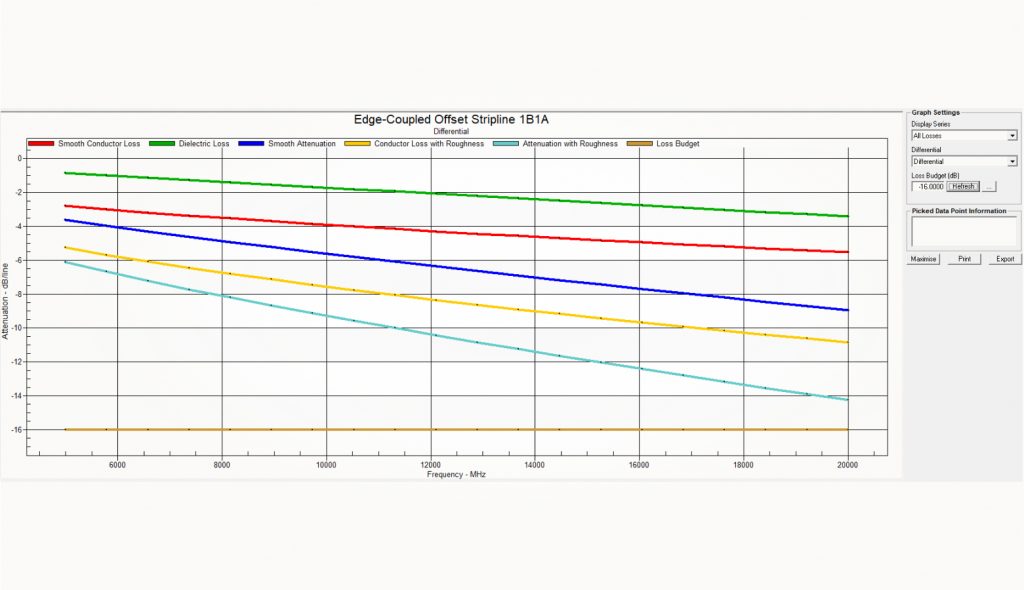
В сетапе используется дифференциальная пара длиной 10 дюймов, шероховатость учтена для слоев проводника и опоры. Естественно, она разная для меди, обращенной в сторону ядра и препрега.

Разница между синим и бирюзовым графиками показывает вклад шероховатости. Несмотря на то, что сетап состряпан «на коленке» и использованные в нем числа совпадают с реальными разве что порядком, мы можем констатировать, что вклад шероховатости в общую картину потерь как минимум достоин отдельного рассмотрения.

Для начала попробуем разобраться в том, с какой стороны подходить к обозначенной проблеме и почему она вообще является проблемой. Следующая диаграмма может иметь очень широкую применимость. Она грубо отражает путь, который можно проделать от постановки задачи до ощутимых практических результатов. Итак:

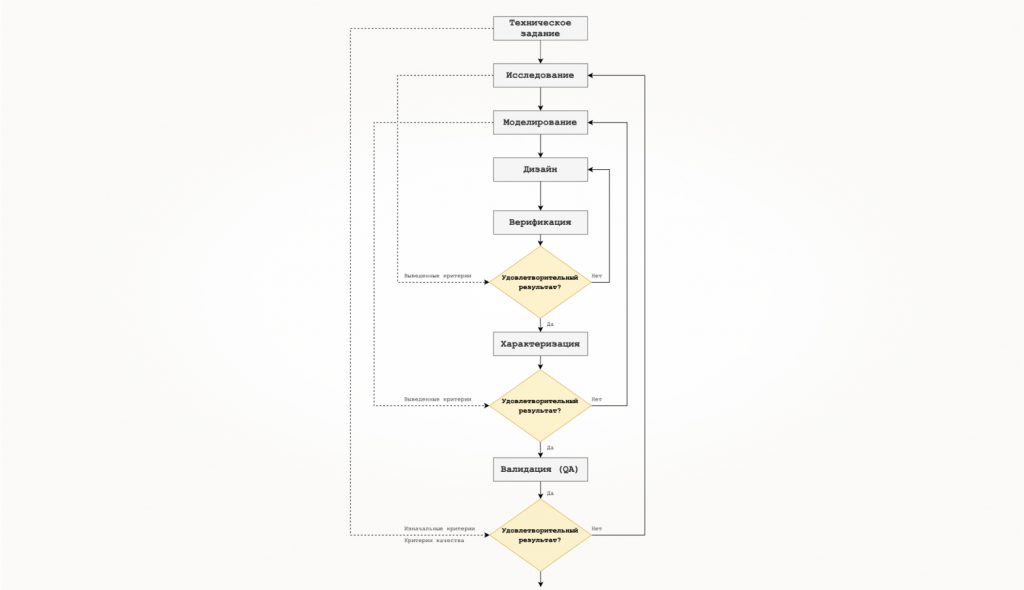
Представленный процесс, разумеется, не является догмой. Он может быть значительно сложнее или проще в зависимости от того, насколько дороги сопутствующие риски. А теперь раскроем каждый этап процесса, чтобы видение превратилось в стратегию.

В нашем случае вопрос технического задания стоит достаточно просто. Тот факт, что в рассматриваемом синтетическом кейсе применяется технология PCIe, может быть отражен в техническом задании в виде требования соответствия базовой спецификации PCIe. Все остальное (включая, естественно, методику испытаний) вытекает из этого требования.

Остальные нюансы мы намеренно опускаем, на что имеем право за счет сделанных ранее допущений.

Теперь нужно определить, какие аспекты потребуют дополнительного внимания, то есть ответить на вопрос: «Что наиболее важно для выполнения поставленной задачи?». Некоторые кандидаты были упомянуты нами ранее: целостность питания, ЭМС, целостность сигналов. Уделив особое внимание вопросу целостности сигналов (и в частности — величине SDD21), мы обнаружили, что шероховатость играет в этом вопросе далеко не последнюю роль.

Мы в первом приближении прикинули, где недостаточно грубых качественных оценок — и шероховатость вошла в «почетный список» нюансов, которые мы хотели бы в больших подробностях учесть на этапе моделирования. Разумеется, пока только на правах гипотезы.

Почему проблема является проблемой, мы поняли именно на этом этапе. Дальше будем постепенно отходить от абстрактного контекста к актуальному.

Теперь нам необходимо составить модель системы. В нашем простом случае речь идет об одной дифференциальной паре. Наша цель — выяснить ее максимальную длину, чтобы удовлетворить требованиям по SDD21. В идеальном мире результаты этого этапа претендуют на хорошую степень достоверности, так как сетап уже не составляется «на коленке», а учитывает целую мириаду факторов. В реальности сам процесс моделирования, строго говоря, состоит из нескольких итераций, хотя мы этого намеренно не показываем. Здесь мы можем учитывать вариации температуры, производственные допуски, можем играться с параметрами стека будущей платы и много с чем еще. В результате получаем набор ограничений и правил, который является вводным для следующего этапа — непосредственной имплементации топологии.

Здесь же мы можем с большей уверенностью понять, насколько важны те или иные параметры моделируемого объекта (дифференциальной пары) за счет проведения анализа чувствительности к изменениям этих параметров. И здесь же можем понять, так ли важно учитывать ту же шероховатость. Но предположим, что все-таки важно и что поставленная нами в ходе исследования гипотеза подтвердилась.

В контексте разработки топологии печатной платы «дизайн» — итеративный процесс работы схемотехника и тополога (часто — нескольких топологов). Результатом процесса, очевидно, является топология печатной платы, пригодная для дальнейшей верификации — с отсутствием грубых и очевидных нарушений, и проверенная топологом и схемотехником, что называется, на свежую голову.

Интересно, что в реальности почти никогда не получается попасть в рамки всех выведенных на более ранних этапах ограничений. В процессе всегда возникают различные «тонкие» места и необходимость компромиссов. По этой причине, а также потому, что ранее разработанная модель не является идеальной, необходим следующий этап — к нему и переходим.

В самых общих терминах верификация нужна, чтобы продемонстрировать жизнеспособность дизайна перед его отправкой на производство. Здесь мы получаем первый явно выраженный и потенциально болезненный цикл — результаты верификации могут являться основанием для пересмотра дизайна. Поскольку мы ранее ввели огромное число допущений, мы можем сказать, что на выходе из процесса верификации нас интересует исключительно SDD21.

Верификация обычно проводится для самого «запущенного» случая — например, самой длинной дифференциальной пары в топологии платы. Для большинства плат такой подход является разумным компромиссом между рисками и ресурсозатратами. После успешного завершения процесса верификации мы отдаем данные платы на завод вместе с набором технических требований, например, по шероховатости. До получения готовой платы с завода происходит немало процессов, которые в том числе могут привести к дополнительной цикличности, но эти нюансы мы затрагивать не будем. Представим, что мы уже все получили либо завод получил первые образцы у себя, и перескочим к следующему этапу.

Суть характеризации заключается в измерении свойств изучаемого объекта, коим в нашем случае является дифференциальная пара. Этот этап выступает звеном обратной связи, чтобы мы могли убедиться, что выбранная ранее модель корректно описывает объект и/или его поведение.

В простейшем случае в рамках процесса характеризации производится проверка соответствия предсказаний модели (SDD21 для дифференциальной пары определенной длины) и результатов измерений. В случае несоответствия и при корректной постановке эксперимента (корректное исключение оснастки, обработка результатов и т. п.) у нас появляются основания для корректировки модели. Также полученные на этом этапе данные позволяют более точно ставить гипотезы на этапе валидации (испытаний).

Ошибки на этапе характеризации еще опасней, чем при моделировании, так как из-за них можно пойти в кардинально неверном направлении на следующей итерации процесса разработки. В конечном итоге при накоплении ошибок на разных этапах продолжение разработки может перестать быть коммерчески оправданным, что в общем-то означает «смерть» проекта.

Валидация, она же QA, она же испытания, — это комплекс мероприятий, который в общем случае призван убедиться, что:

• Устройство соответствует техническому заданию (в идеальном мире).
• Устройство функционирует с определенной производительностью в диапазоне внешних условий (когда ТЗ как такового нет, но есть представление, что должно быть «не хуже чем…»).

Если наблюдаемая на этом этапе реальность не соответствует ожиданиям, важно правильно поставить гипотезу о причинах отклонения и по возможности провести проверку выдвинутой гипотезы. Неверный техпроцесс или неверно подобранный тип фольги (повышенная шероховатость является последствием и того, и другого) могут:

• Быть причиной повышенного SDD21 и невозможности достичь нужных скоростей передачи данных.
• Привести к нестабильности показателей производительности: работает в двух произведенных платах из десяти, работает в недостаточно широком диапазоне температуры или влажности и т. п.

Валидация, обработка ее результатов и принятие решений на ее основе — чрезвычайно сложный процесс. Это обусловлено охватом самой процедуры — мы буквально проверяем все, что поддается проверке. В нюансы вдаваться не будем, но обеспечение тестируемости и обеспечение тестового покрытия в том числе на этапе разработки архитектуры (DFT, или Design for Testability) — отдельная история. Предположим, что мы заранее обеспечили тестируемость и локализуемость всего или почти всего, что может быть нам интересно.

В ходе валидации высокоскоростных интерфейсов мы имеем возможность оценить «открытость» глазковой диаграммы интерфейса и проверить ее на предмет соответствия требованиям соответствующих спецификаций. При неудовлетворительных результатах валидации проблемы с шероховатостью могут быть одной из рабочих гипотез. А за счет проведенной ранее характеризации соответствующие гипотезы можно выдвигать со значительно большей уверенностью.

Итак, мы наконец-то получили ответ на вопрос «зачем?». Очень краткий итог всего пройденного на данный момент:

• Шероховатость медной фольги в печатной плате оказывает влияние на работу высокоскоростных интерфейсов.
• Чтобы учитывать это влияние, необходимо выбрать модель, адекватно описывающую само явление.
• Чтобы понять, что потенциальные проблемы сводятся к шероховатости, нужно обеспечить характеризуемость итоговой структуры линии передачи и локализуемость причин этих потенциальных проблем.

Сосредоточимся теперь на стадии моделирования и в частности на выборе модели. Рассмотрим популярные модели влияния шероховатости на высокочастотные потери в проводнике.

Модели, описывающие влияние шероховатости на высокочастотные потери, которые мы будем рассматривать, условно делятся на феноменологические (это не совсем эмпирические, так как эмпирическим, строго говоря, не нужна теория) и модели, которые выводятся из фундаментальной физики (наподобие уравнений Максвелла). Феноменологические модели не имеют под собой физического базиса практически по определению, но они все равно могут выдавать приемлемый в контексте поставленной задачи результат.

Сразу зададим себе вопрос: что считать «приемлемой» моделью? Ранее мы увидели, что ошибки на любом этапе проектирования (в том числе на этапе моделирования и характеризации) имеют свою цену. Оказывается, что критерии «приемлемости» сводятся к балансу рисков, и в итоге — к специфике проекта. Например, в дизайнах в которых нет ничего быстрее PCIe Gen3, многое из того, о чем идет речь в статье, часто вообще не нужно. Риск можно измерить в деньгах и рассчитать по формуле [вероятность события]*[финансовые потери при его возникновении]. На другой чаше весов — время, которое, как известно, тоже достаточно прямолинейно конвертируется в деньги.

Специфику нашего воображаемого кейса мы уже обозначили в предисловии, теперь настал момент зафиксировать, как она будет влиять на выбор модели. Условимся на следующем:

• Мы не хотим проводить раннюю характеризацию материалов и структур, то есть делать это до заказа первых образцов разработанного модуля на фабрике.
• Отсюда следует, что у нас нет роскоши использовать модели, которые сильно полагаются на «подгонку» коэффициентов и параметров, чтобы соответствовать результатам измерений.
• Желательно, чтобы в модели использовались параметры, доступные документации на фольгу и/или химию (техпроцессы), используемые на целевой фабрике. А именно — одно или более из следующего:
  • R_a — среднее арифметическое значение профиля z (x, y),
  • R_q — среднеквадратическое значение профиля z (x, y),
  • R_z — средняя разница между самой глубокой впадиной и самым высоким пиком профиля, которая обычно берется по 10 «худшим» точкам,
  • RSAI — характеристика соотношения площадей реальной и идеальной поверхностей.

Теперь наконец приступаем к разбору популярных моделей.

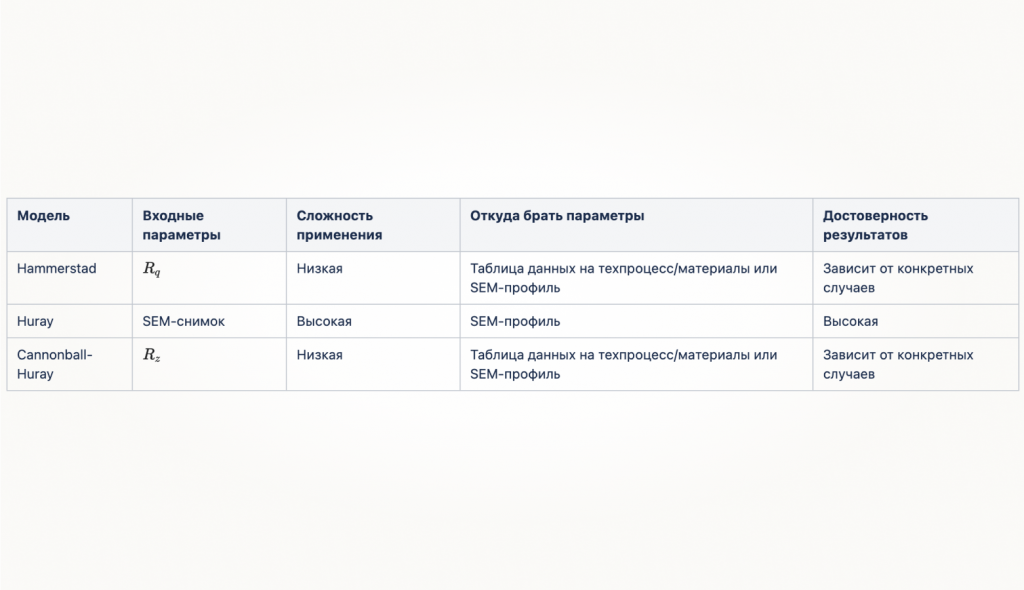
Получение SEM-изображения не всегда оправдано с точки зрения затрачиваемых на эту процедуру средств, поэтому SEM-изображения у нас часто не будет. А даже если будет, то применение Hurray-модели в чистом виде все равно останется не самой тривиальной задачей: профиль впоследствии придется разложить на суперпозицию сфер, что само по себе значительно сложнее, чем получение R_z или R_q из z (x, y).

При отсутствии данных о профиле фольги z (x, y) среди рассмотренных ранее моделей применимыми остаются только две: модель Хаммерстада и модель Cannonball-Hurray. Обе основаны на допущениях, у обеих есть пределы применимости. Чтобы принять решение, какую и когда использовать, надо рассмотреть, что за допущения существуют для каждой модели и каковы их последствия.

В случае модели Хаммерстада все сводится к одному параметру — R_q, среднеквадратическому от профиля z (x, y) по некоторой области образца.

Она основывается на еще более старой модели Моргана 1949 года, которая строится на предположении о том, что высокочастотный ток за счет скин-эффекта течет «вдоль» зазубренной поверхности, где зазубрины, как тогда предполагалось, достаточно хорошо описывают профиль шероховатой фольги. Зазубрины в модели Моргана появились не просто так — речь тогда шла буквально о выцарапанных ножом зазубринах на поверхности экспериментального образца. В оригинальной статье исследуются не только пилообразные зазубрины, но именно они перекочевали в модель Хаммерстада.

Очевидный недостаток модели Моргана в том, что в реальной жизни ток совершенно не обязан течь перпендикулярно зазубрине, да и шероховатой медь на заводе делают далеко не ножом. Модель Хаммерстада решила эту проблему на удивление просто: она подразумевает, что z (x, y) не зависит от поворота системы координат вокруг Oz, то есть профиль всегда (в любом направлении) выглядит как на иллюстрации ниже:

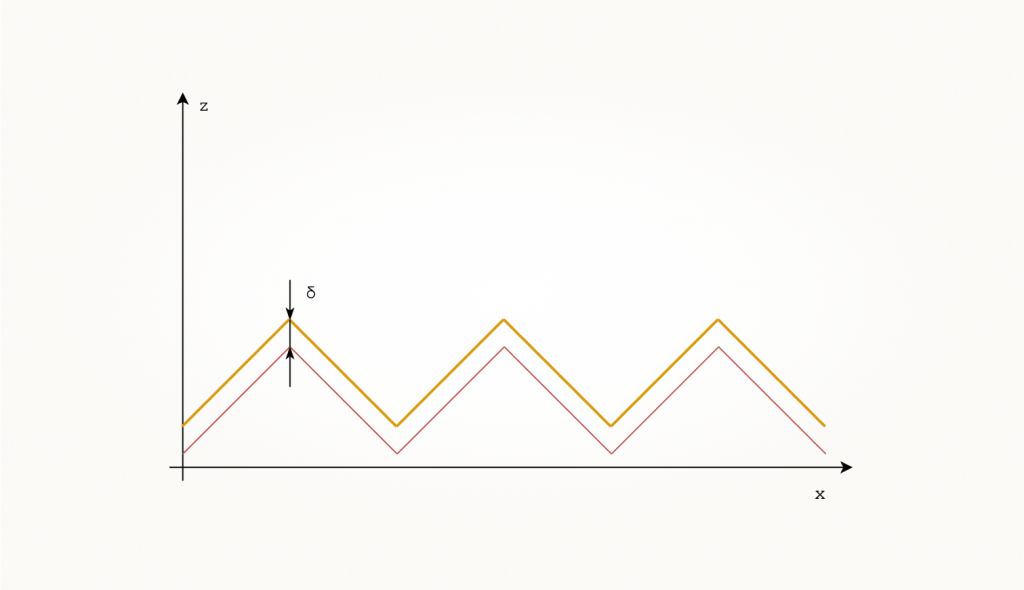
Теперь внимательно присмотримся к «математике Хаммерстада»:

R_{ac} = K_{h}R_{s}\sqrt{f},,
K_{h} = 1 + \frac{2}{\pi}\arctan{[1.4(\frac{R_{q}}{\delta})^2]},,

где:

• f — нормированная на 1 Гц частота,
• R_s — аттенюация на гладкой поверхности,
• R_ac — аттенюация на шероховатой поверхности,
• K_h — коэффициент Хаммерстада,
• δ — глубина скин-слоя,
• R_q — среднеквадратическое отклонение от плоской поверхности.

Арктангенс во втором выражении, являющемся коэффициентом Хаммерстада, доберется до π/2 тем быстрее, чем выше R_q и чем выше частота (поскольку это означает малый скин-слой δ). Мы получаем картину, при которой с ростом частоты влияние шероховатости на вносимые потери ослабевает: потери становятся пропорциональны квадратному корню частоты (см. первое выражение), а чувствительность потерь к изменениям частоты уменьшается, в пределе стремясь к нулю. Это контринтуитивно и не соответствует наблюдениям. Условная граница применимости модели Хаммерстада: f < 4 ГГц и R_q < 5 мкм.

Можно ли расширить эту условную границу? В 2011 году Юрий Шлепнев et al. в своей работе «Roughness Characterization for Interconnect Analysis» показал, что это возможно. Мотивация для написания этой статьи хорошо описана в одном из последних предложений введения:

Так родилась модифицированная модель Хаммерстада. Есть, впрочем, нюанс, который станет ясен после чуть более детального рассмотрения самой модели.

Суть модифицированной модели Хаммерстада заключается в видоизменении коэффициента K_h. Теперь он выглядит так:

Новый параметр RF характеризует максимальное увеличение потерь в проводнике за счет эффектов шероховатости. Именно такое математическое представление было, по всей видимости, вдохновлено формами графиков измеренной частотной зависимости потерь и предсказанной оригинальной моделью.

Первая попытка придать новоиспеченной модели физический смысл основывалась на предположении, что RF также может быть измерен механически как среднее увеличение пути вдоль шероховатой поверхности по сравнению с плоской поверхностью («RF can also be mechanically measured as the average increase in path along the rough surface as compared to a flat surface»). Попытка оказалась провальной, а об остальных мы не осведомлены, даже если они были. Попытка же подогнать (намеренно без кавычек) коэффициенты, чтобы получить хорошее схождение графиков, оказались успешнее.

«Нюанс» в итоге заключается ровно в том, что без проведения измерений (характеризации) ключевой параметр данной модели — RF — остается в серой зоне. Получить его можно либо методом проб и ошибок, либо за счет проведения ранней характеризации отдельных образцов материалов, прошедших к тому же через целевой техпроцесс. Статистику и допуски пока оставляем за скобками.
Резюмируя, модель Хаммерстада имеет ограниченную применимость, а ее модифицированные мутации используют неизвестные и во многом абстрактные параметры. В некоторых случаях эти модели полезны, но мы ими не пользуемся.

Модель Cannonball-Hurray рассмотрим начиная с оригинальной (Hurray). В течение долгого времени индустрия комфортно жила с моделью Хаммерстада. Конечно, человечество давно разрабатывает электронику с частотами, превышающими 70 ГГц, но в мире высокочастотного аналога с очевидно более развитой культурой характеризации всегда можно было «подогнать» коэффициенты модели к результатам измерений и в целом позволять себе выделять время для подобных активностей.

В мире HSD (High Speed Digital) стараниями некоторых крупных представителей индустрии высокоскоростные интерфейсы долгое время в массе своей стагнировали. Для разработки устройств с условным PCIe можно было обходиться вообще без учета шероховатости либо номинально использовать модель Хаммерстада, причем без всяких модификаций. Частоты интереса составляли всего лишь 4 ГГц, а типичные (если специально не указывать тип фольги в техтребованиях) R_q — порядка 7−12 микрон. Как мы ранее выяснили, модель Хаммерстада даже здесь уже показывает расхождения с реальными измерениями, но их влияние на работу изделий вычислительной техники оказывалось пренебрежимо малым.

С приходом в индустрию технологий PCIe Gen4 и Gen5 (8 и 16 ГГц, соответственно) появились и новые вызовы, и в качестве ответов на них — новые модели, объясняющие потери, обусловленные шероховатой поверхностью проводника в совершенно ином ключе. Пол Хурей в своей книге под названием «The Foundations of Signal Integrity» и впоследствии — в рамках выступления на DesignCon 2010 с темой «Impact of Copper Surface Texture on Loss: A Model that Works» предложил модель, названную в честь ее автора — Модель Хурея (Huray Model). Рассмотрим вкратце, почему, по мнению Хурея, модель Хаммерстада нежизнеспособна и что именно Хурей предложил в качестве альтернативы.

Одним из существенных недостатков модели Хаммерстада являлось и является отсутствие физического базиса. Этот недостаток и основополагающее предположение модели о том, что высокочастотный ток «проделывает более длинный путь по неровной поверхности», в конечном итоге можно использовать, чтобы доказать теоретическую несостоятельность модели.

Ниже приведен ранее фигурировавший здесь рисунок пилообразного профиля медной фольги. Представим, что в направлении оси Ox распространяется электромагнитная волна и обозначим на нем следующие величины:

• E — напряженность электрического поля.
• Σ — поверхностная плотность электрического заряда.
• c — скорость света в вакууме.
• v — скорость «перемещения заряда» вдоль поверхности проводника.

Условимся, что диэлектрическая постоянная среды распространения у нас равняется четырем, тогда скорость распространения электромагнитной волны в среде будет в 2 раза (√4) меньше скорости света в вакууме. Магнитную составляющую волны иллюстрировать не будем, чтобы не захламлять рисунок.

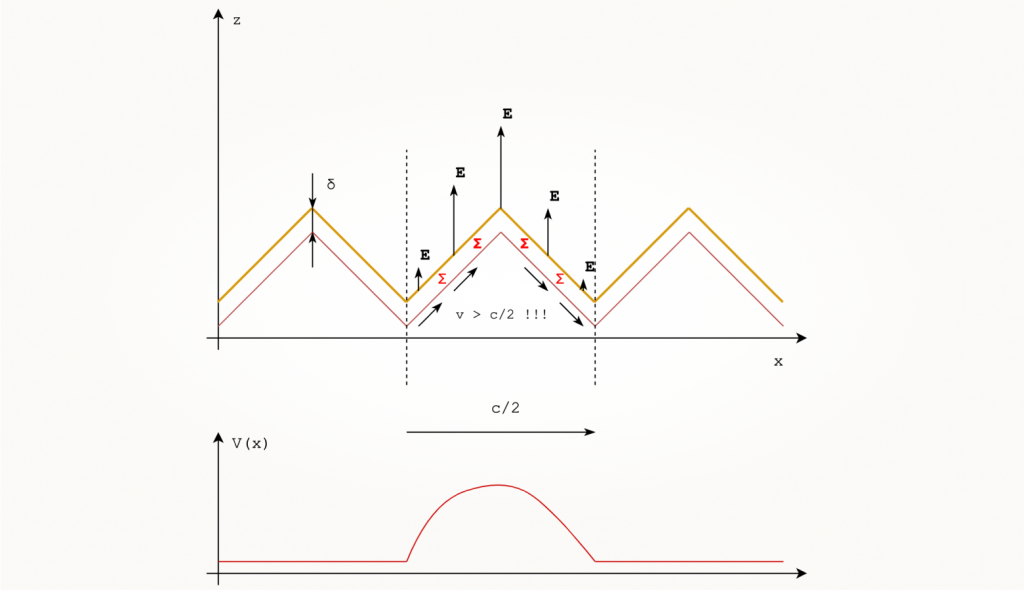
В соответствии с теоремой Гаусса, чем больше напряженность электрического поля, тем больше должна быть плотность поверхностного заряда Σ. То есть для поддержки переменного электрического поля поверхностный заряд вдоль неровной поверхности меди должен перераспределяться, что, казалось бы, соответствует протеканию тока вблизи поверхности проводника. Не будем, однако, забывать, что в нашем случае электромагнитная волна распространяется в среде со скоростью c/2, тогда как мы все еще считаем, что ток течет по более «длинному» пути.

Возникает несостыковка. Мы получаем, что:

• Скорость перемещения заряда вдоль поверхности проводника v должна превышать скорость света в среде.
• Эта же скорость v может запросто превысить скорость света в вакууме, если взять достаточно шероховатую поверхность и/или среду с достаточно низкой диэлектрической проницаемостью.

Этот и ряд других доводов Хурей счел достаточными, чтобы поставить крест на модели Хаммерстада. Модель, предложенная Хуреем взамен, строится вокруг теории поглощения и рассеяния электромагнитных волн сферическими проводниками в вакууме проводящими сферами. Хурей в своем рассмотрении считал, что энергия электромагнитного поля поглощается и рассеивается проводящими сферами и именно эти процессы обуславливают потери на неровной поверхности проводника, которая, как несложно догадаться, в модели Хурея выглядит как множество проводящих сфер. То есть примерно как на следующем рисунке:

Если присмотреться к типичному SEM-снимку, на нем и правда можно увидеть множество сфер и представить, что неровности описываются определенной конфигурацией этих самых сфер:

Кроме того, Хурей et. al. при помощи Оже-спектроскопии выяснил, что поверхности медных сфер покрыты пленкой, в которой присутствуют углерод, кислород, кремний и немного никеля. Из этой находки последовал вывод о том, что заряд в индивидуальных сферах можно считать изолированным и что проводимость между сфер относительно невелика.

Далее необходимо вычислить сечение поглощения и рассеяния для данной конфигурации сфер. Хурей решает эту задачу рассеяния (scattering problem) методом парциальных волн, который сложно объяснить простыми словами. Результатом решения этой задачи становятся сечения поглощения и рассеяния. Каждая из этих величин показывает, какая доля энергии приходящей волны была «потрачена» на соответствующие взаимодействия. «Потрачена» — не самое верное слово для рассеяния, но Хурей показывает, что на частотах ниже 100 ГГц рассеянием можно пренебречь. Что и делаем.

Итоговое выражение, характеризующее долю потерь энергии, обусловленную шероховатостью, получается следующим:

\frac{P_{rough}}{P_{smooth}} \approx 1 + \frac{3}{2}\sum_{i=1}^j (\frac{N_{i}4\pi r_{i}^2}{A_{hex}})/[{1 + \frac{\delta}{r_{i}} + \frac{\delta^2}{2r_{i}^2}}],,

где:

• N_i — число сфер с радиусом ri в пределах шестиугольной области поверхности проводника с площадью Ahex (шестиугольник выбран произвольно и не влияет на итоговый результат),
• δ — глубина скин-слоя,
• A_hex — площадь условно элементарной ячейки (в данном случае — шестиугольника), к которой мы вскоре вернемся.

Теперь попытаемся свести все допущения, лежащие в основе модели и оценить ее применимость для «кейса в вакууме». Итак:

• Неровности на поверхности меди должны быть похожи на множество сфер. Справедливо для технологических процессов из 2000-х годов, но может быть несправедливо для так называемых low etching процессов, которые хочется использовать в действительно высокоскоростных дизайнах (112/224 ГТ/c PAM4 и более).
• Проводящие сферы должны быть изолированы друг от друга, то есть должно быть верным предположение о непроводящей (или плохо проводящей) пленке, покрывающей сферы. Иными словами, взаимодействие сфер должно быть достаточно незначительным, чтобы им пренебречь.
• Ряд допущений, описанных самим Хуреем, заключается в игнорировании эффектов второго порядка. Им же было показано, что вклад этих эффектов составляет не более 6%, то есть часто является пренебрежимо малым.

Хурею удалось экспериментально подтвердить свою модель, хоть это и тяжело проверить самостоятельно. В статье «Impact of Copper Surface Texture on Loss: A Model that Works» приводятся изображения поверхности проводника в изометрии и рядом — графики, где предсказания модели очень хорошо совпадают с измерениями. Также приведены параметры, поданные на вход модели, — радиусы и число сфер. Мы не пытались посчитать число сфер и их радиусы по фотографии, оставив валидность модели Хурея вопросом веры.

Модель Хурея ценна за счет следующих обстоятельств:

• В отличие от модели Хаммерстада, она не основывается на неверных (и даже местами наивных) представлениях о поведении электромагнитных волн.
• Показано, что при помощи модели можно достаточно точно оценивать вклад шероховатости в потери в широком диапазоне частот (вплоть до 50 ГГц и выше).

Чтобы облегчить применение модели, Хурей предлагает еще одно упрощение — Uniform snowball model, или «Модель одинаковых сфер». Суть заключается в следующем:

• Выделяем на SEM-снимке некую повторяющуюся (в плане числа и распределения сфер) область.
• Вычисляем средний радиус сфер в рамках выделенной области.
• Выбираем число сфер в области так, чтобы можно было этим числом сфер примерно воспроизвести неровности поверхности проводника.

При желании можно не прибегать к вычислению среднего радиуса сфер. Например, имеет смысл использовать в расчетах два вида радиусов, если соответствующие сферы явно выражены на снимке. Также стоит отметить, что Хурей в качестве «области» использовал шестиугольник, поскольку эта форма соответствовала имеющимся у него снимкам. Однако, в теории, конкретная форма на конечный результат влиять не должна.

Двигаемся дальше по спирали упрощений. Мы уже упоминали, что не у всех и не всегда есть возможность получить SEM-снимки и выискивать похожие на них объекты на сфере. Перечитаем еще раз Хурея и предположим, что неровности поверхности проводника выглядят как шестиугольные пирамидки. Также вспомним одно любопытное обстоятельство — наивысшая плотность упаковки сфер достигается при так называемой гексагональной плотноупакованной решетке. Совпадение? Инженер-технолог Берт Симонович так не думает.

Исходя из чисто геометрических соображений, Симонович предлагает в качестве отправной точки подавать на модель Хурея параметры, связанные с параметрами фольги, которые можно найти в документации на фольгу и/или техпроцесс по ее обработке, следующим образом:

N = 11,,
r \approx 0.055 R_{x},,
A_{hex} \approx 25.684r^2,,

где:

• N — число сфер с радиусом r,
• R_x — или R_a, или R_z; в оригинальной статье отсутствует внятное объяснение, от чего в рамках используемой модели зависит выбор одного или другого,
• A_hex — площадь основания шестиугольной пирамиды, которая формируется из этих сфер.

Ранее приведенное уравнение Хурея с этими допущениями вырождается в следующее:

\frac{P_{rough}}{P_{smooth}} \approx 1 + 66 (\frac{\pi r^2}{A_{hex}})/[{1 + \frac{\delta}{r} + \frac{\delta^2}{2r^2}}]..

Очевидно, что с ранее обозначенными предположениями о связи r и A_hex с R_a или R_z можно, как утверждает автор модели, оценить влияние шероховатости на потери на основании только лишь соответствующих параметров, которые обычно вполне себе доступны, так как легко поддаются измерению.

Если выражаться максимально политкорректно, модель Симоновича как бы говорит: «Если не знаете параметров для модели Хурея, возьмите вот эти, конкретные». Излишне говорить, что его подход вызывает немало вопросов. Также неудивительно, что, помимо вопросов, модель также притягивает немало критики.

Пожалуй, единственным достоинством модели является ее простота. Скорее всего, эта простота обманчива, но решение о ее применении принимается «по месту» — на основании оценки цены ошибки в каждом конкретном случае. То же самое можно сказать про любую другую модель. Что действительно важно понимать перед принятием решения, так это (как обычно) тяжесть последствий этого решения.

Теперь рассмотрим простой, но показательный кейс со следующими вводными:

• Задача — спроектировать серверную материнскую плату под применение в «типовом» rack-сервере.
• Целевой процессор поддерживает PCIe Gen5 (более правильно — скорости передачи до 32 ГТ/с).
• К одному из PCIe-портов процессора нужно подключить сетевую карту 400 GbE в форм-факторе OCP 3.0 (например, 900−9X7AX-004NMC0 от NVIDIA) и, естественно, иметь возможность полностью реализовать ее потенциал.

Компоновка (floorplan) современного сферического сервера в вакууме, скорее всего, будет выглядеть, как показано на приведенной ниже диаграмме. Такая компоновка обусловлена многими факторами, среди которых присутствуют эффективность доставки электропитания до периферии и охлаждение. Эти нюансы мы пока что оставим за скобками. Райзеры и SMP-шины для чистоты изложения не показаны.

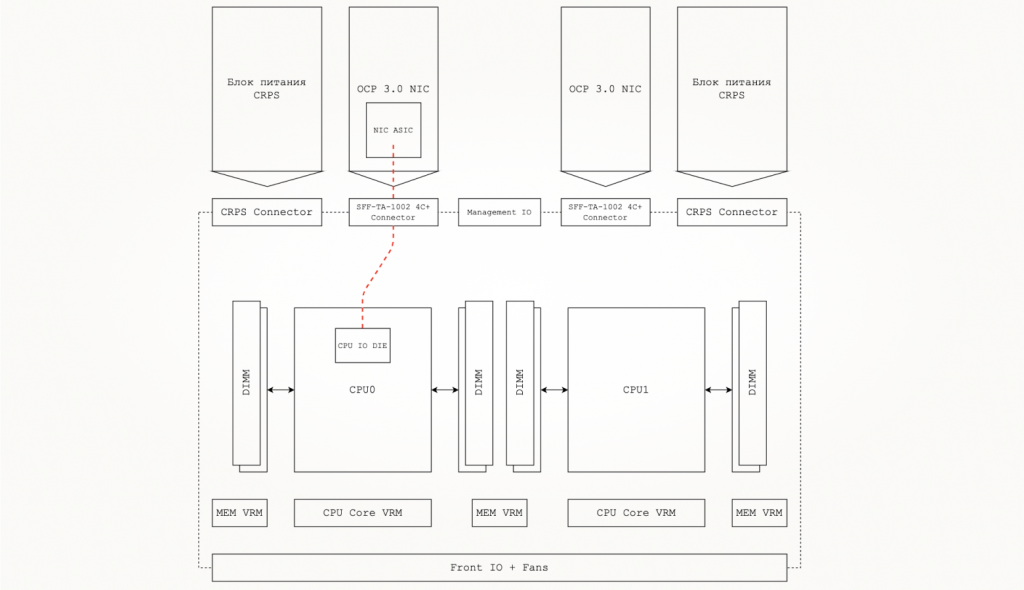
Интересующий нас тракт специально выделен красным в бесцветной диаграмме. В спецификации PCIe фигурирует (причем даже не в качестве нормативного) значение потерь на включение от бампа кристалла передатчика до кристалла приемника. Поэтому интересующий нас тракт начинается на подложке и заканчивается на подложке, охватывая не только платы и коннекторы. Имея представление о внутренней компоновке разрабатываемого устройства, мы можем приступать к декомпозиции потерь в высокоскоростном тракте. С учетом подложек корневого комплекса (здесь и далее — RC, или Root Complex) и оконечной точки (здесь и далее — EP, или Endpoint), получаем следующую, все еще упрощенную декомпозицию тракта:

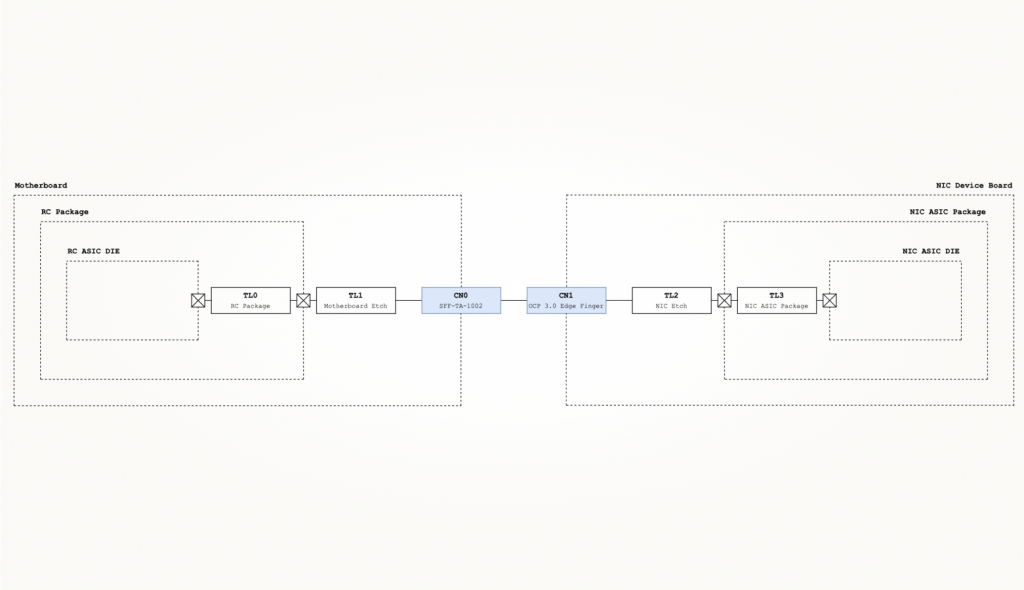
Далее, вооружившись релевантными спецификациями (PCIe Base Specification, SFF-TA-1002, OCP 3.0 NIC), составляем пессимистичную картину потерь в тракте. Без характеризации элементов тракта у нас нет оснований пользоваться иной:

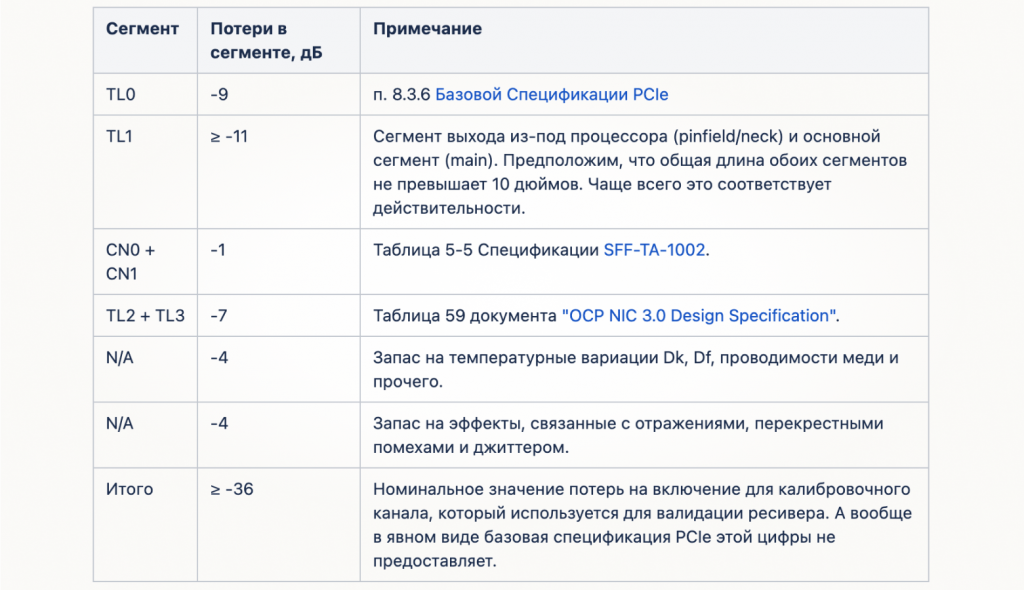
Далее наступает момент, когда нам необходимо начинать более углубленное планирование топологии и расчет стека. Часто в этом деле помогают референс-дизайны, но не всегда. И более того — иногда авторы референсов принимают откровенно сомнительные решения, которые могут приводить к не самым приятным последствиям. Из-за NDA расписать не получится, но глобальный посыл прост: критическое отношение, в частности, к референсам является необходимым условием для принятия ответственных решений.

Некоторые читатели могут быть знакомы со статьей, которая рассказывает, как мы считали стеки в далеком 2017 году. Описанная в статье методика во многом актуальна с тем лишь дополнением, что в процесс добавляется статистический анализ разрабатываемых конструкций. Иными словами, мы теперь чаще и более осознанно стремимся делать стеки, слабо подверженные влиянию таких фаз Луны, как температура, усадки препрега, допуск на подтрав и прочих. Также не стоит забывать, что универсальных решений для каждого случая не существует. К примеру, пытаясь минимизировать потери на включение, мы усугубим проблему перекрестных помех, причем порой в самых неожиданных местах. Например, если у DDR отражения из-за низкого D_f материала затухают «долго», DDR’у то этого только поплохеет, хотя мы всего лишь пытались облегчить жизнь шине PCIe.

Предположим, что одним из итогов длительного и нелегкого процесса конструирования стека стала следующая геометрия 85-омной дифференциальной пары:

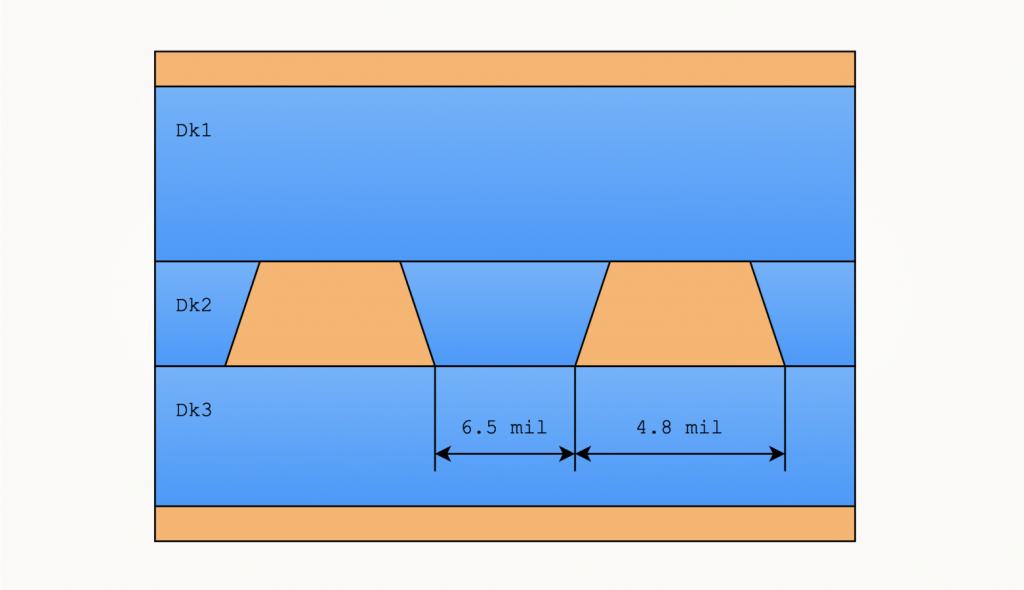
Далее мы практически априори знаем, что нам нужна низкая шероховатость. Это означает одно или более из следующего:

• В технических требованиях на плату будет фигурировать HVLP/VLP-фольга и конкретное значение как минимум одного ключевого и измеримого параметра шероховатости фольги (R_q, R_z, RSAR или RSAI).
• В технических требованиях на плату будет присутствовать требование использовать специализированную химию, чтобы изменения оригинального профиля фольги были минимальны.

Если фабрика соблюдает указанные технические требования, то ожидаемые SEM-снимки меди до и после процессов подготовки к нанесению фоторезиста и подготовки к прессованию будут выглядеть ориентировочно следующим образом:

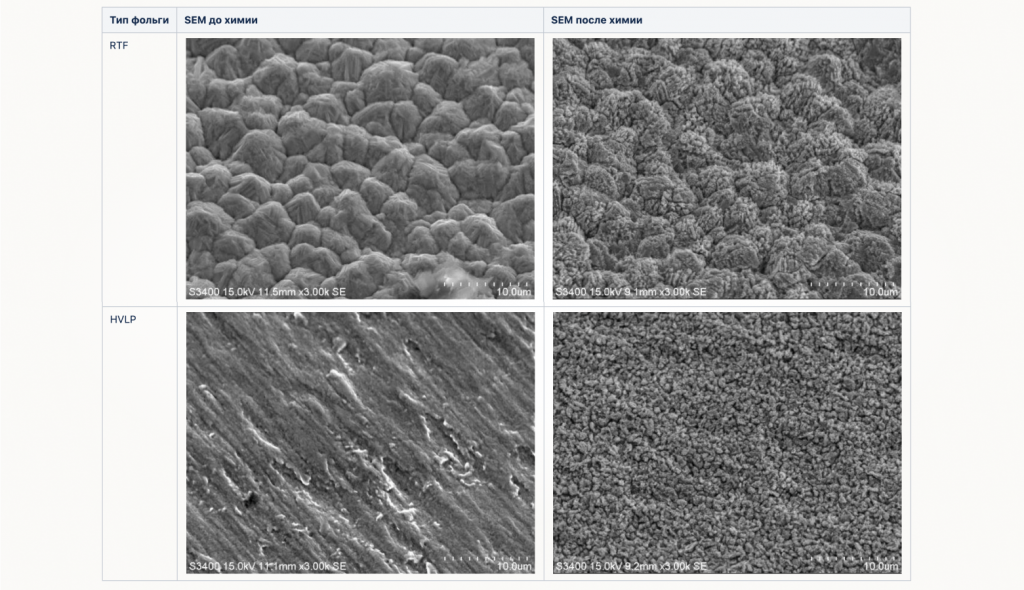
Хорошим показателем качества используемой химии является финишный RSAI или RSAR. Этот показатель является характеристикой соотношения площади реальной поверхности (или правильнее сказать дельты) к площади гладкой поверхности. Вычисляется следующим образом:

RSAI = \frac{A}{A_{flat}} - 1..

Для условно качественной химии этот показатель находится между 0.2 и 0.3. Для HVLP меди до обработки — порядка 0.08−0.1 со стороны препрега.

Подобного рода SEM-изображения дают чуть больше уверенности в применимости модели Cannonball-Hurray, даже несмотря на ее ограничения. Поэтому, и отчасти за неимением альтернатив без характеризационных данных, используем ее. В том же софте, в котором считали стек и геометрии TL, организуем небольшой сетап для условно «лучшего» и условно «худшего» случаев. Описание сетапа примерно такое:

Напомним, что единственным параметром Cannonball-Hurray после всех допущений остается R_z изучаемой поверхности.

В итоге для «лучшего» и «худшего» случаев получаем следующие результаты:

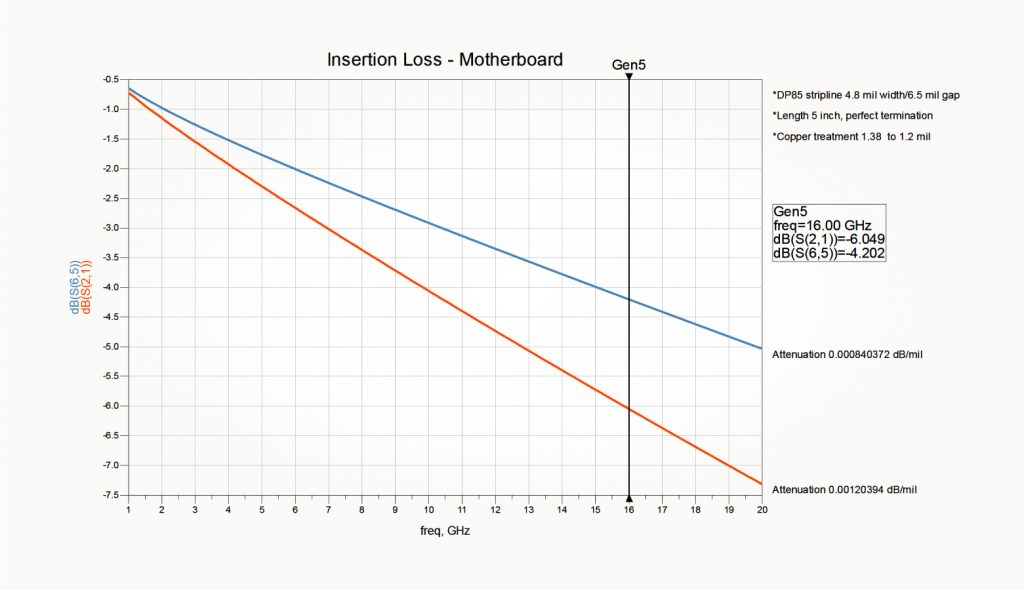
Здесь уже можно формировать требования к предельно допустимому финальному R_z. Вспомним, что ранее мы ограничили себя максимальной длиной диффпары, равной 10 дюймам, и что контролируемые нами потери не должны быть хуже -11 дБ. Получаем, что предельные погонные потери составляют 1.1 дБ/дюйм. В нашем случае это значение погонных потерь примерно соответствует шероховатости 3 мкм R_z. При формировании реальных технических требований мы, конечно, не используем примерные значения, но они прекрасно подходят для иллюстративных целей.

Следующими большими задачами будут валидация дизайна силами QA и параллельно — характеризация линий передач на полученных платах на специализированных купонах, которые формируются на тех же производственных заготовках, что и сами платы. Данные характеризации послужат для уточнения используемых моделей. В дальнейшем это позволит более точно формировать технические требования, принимать более осознанные решения при дизайне PCB, уменьшать неопределенность расчетов и в конечном итоге — достигать более эффективных с точки зрения бизнеса результатов (потенциально дешевле, быстрее, с меньшим риском ошибиться).

Характеризация линий передачи на частотах порядка 16 ГГц — достаточно сложная тема, являющаяся предметом отдельного детального рассмотрения. Если вам интересно почитать о ней, дайте знать в комментариях.