
Готовимся к Micromouse: как роботу построить карту лабиринта

Уже почти 50 лет в разных странах мира проводятся соревновании по робототехнике в дисциплине Micromouse, где роботизированной мыши нужно как можно быстрее найти путь в центр лабиринта и понять, что центр достигнут. В 2023 году Micromouse вошла в программу фестиваля «РобоФинист» в Санкт-Петербурге. А в 2024 году команда Дениса Логашова, инженера-исследователя отдела автоматической обработки результатов моделирования и визуализации YADRO, заняла на соревновании второе место. В этой статье Денис расскажет о сути соревнования и рассмотрит его прохождение в ракурсе используемых алгоритмов.

- как проводятся соревнования Micromouse
- какие этапы прохождения выделяют сегодня
- как написать код для построения карты лабиринта по правилу левой руки
- как оптимизировать код при помощи модульной арифметики
Я работал в паре с другим инженером и отвечал за программную часть робота. По моим наблюдениям, меньше половины участников соревнования поняли задачу соревнования, а остальные создали типичный алгоритм прохождения лабиринта, где предусмотрен только один путь от старта до финиша. Поэтому в серии своих постов я расскажу, какие подходы использовал сам, чтобы решить комплексную задачу Micromouse — исследование лабиринта, построение карты и поиск кратчайшего пути.
Суть соревнования
В нашем варианте лабиринт строится на поле размером 16×16 ячеек. Ячейки квадратные, размер грани составляет 18 см. Зафиксирована точка старта: робот начинает в конкретной ячейке, повернутым в конкретном направлении. Точка финиша — это, как правило, квадрат 2×2 ячейки с одним или несколькими входами.
Задача робота — найти кратчайший путь от старта до финиша и проехать по нему. Обновлять микрокод робота после демонстрации схемы лабиринта запрещено. На решение дается ограниченное время, за которое мышь может проходить лабиринт неограниченное число раз. Поэтому обычно робот сначала строит карту лабиринта, а потом уже пытается доехать до финиша по кратчайшему пути. Более подробно о соревнованиях Micromouse в целом можно почитать в другом тексте на Хабре.
Далее в статьях я буду описывать логику, исходя из того, что читатели знакомы с основами программирования — переменными, циклами, функциями и условиями. Робот, которого мы программируем, способен проехать вперед ровно одну ячейку лабиринта и повернуть на 90 градусов в любом направлении. Он оснащен тремя датчиками расстояния, которые расположены слева, спереди и справа.

Анализ карты лабиринта
Как я писал выше, обычно роботы начинают со сканирования карты. Чтобы сохранять данные о перегородках, мы будем пользоваться битами и битовыми операциями.
Любое число можно представить в виде последовательностей бит, то есть байтов. Ими мы и будем пользоваться в программе. Один байт содержит восемь бит: минимальное возможное число — 0b00000000 (это число 0, если мы говорим про беззнаковые числа), а максимальное число — 0b11111111 (это 255). 0b в этой записи показывает, что мы представляем число в виде последовательности бит.
Числами в их стандартном понимании мы оперировать не будем — нам это попросту не нужно. Мы рассматриваем каждый бит как некое состояние, true или false. В рамках одного байта получается восемь значений, которые могут нам сказать, выполняется ли некоторое условие или нет.
Условимся, что каждый бит в байте отвечает за наличие стенки с одной из четырех сторон вокруг робота. Если стенка есть, бит равен 1, если нет, то 0. Байты считаются справа налево. Четвертый бит в байте отвечает за верхнюю стенку (при взгляде на лабиринт сверху), третий — за правую, второй — за нижнюю и первый — за левую. Такие битовые записи называют масками, и далее мы будем использовать понятие «маска стенки». Значения первых четырех бит рассмотрим позже.
Для удобства добавим все эти маски в переменные:
Будем считать, что изначально вся наша карта не имеет никаких стенок, то есть значения всех бит равны 0. Пусть исходный лабиринт имеет размер 5×5 ячеек:

Псевдокод для его инициализации выглядит следующим образом:
Основные операции с картой
Как нам устанавливать значения для стенок и потом проверять их? Воспользуемся битовыми операциями: нам понадобится побитовое ИЛИ (|) и побитовое И (&). Таблица истинности для них выглядит так:
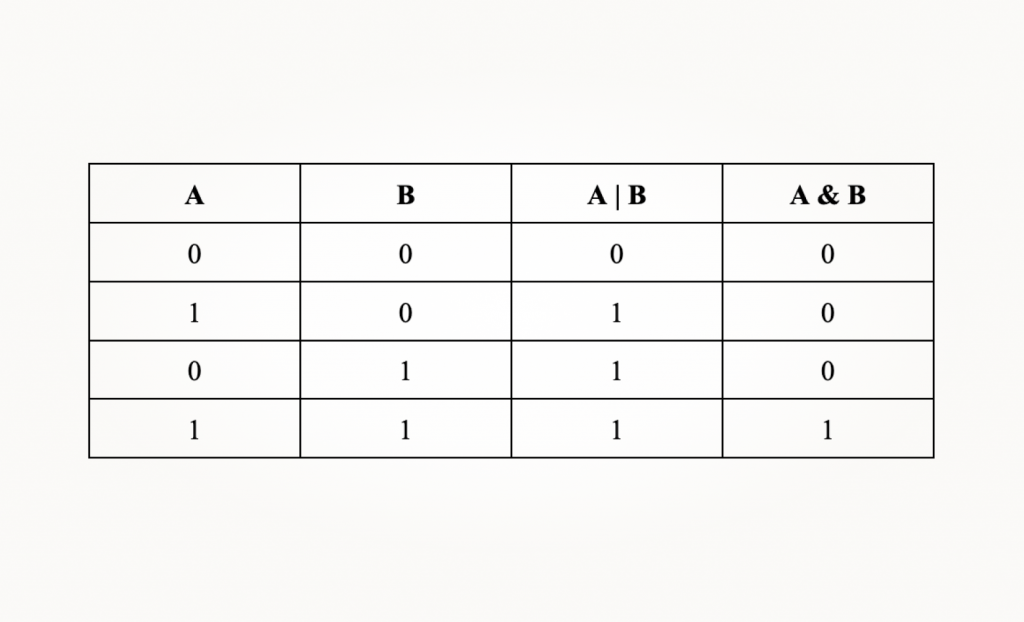
При побитовом ИЛИ мы получаем 1 в итоговом значении, если хотя бы один бит был равен 1. При побитовом И мы получаем 1, только если оба бита равны 1. Как эти операции применяются в нашем случае? Находясь в ячейке, робот считывает значения с датчиков, которые проверяют наличие стенок вокруг. Затем при помощи побитовой операции ИЛИ он может добавить соответствующую стенку в значение для текущей ячейки.
Напомню, что исходный размер лабиринта — 5×5 ячеек. Мы заранее можем выставить значения для внешних стенок. Например, для всех верхних стенок (если смотреть на лабиринт в двумерной проекции сверху) нужно воспользоваться маской up_wall (0b00001000). К исходным нулевым значениям мы добавляем новые с помощью операции ИЛИ:
Далее берем маску правой стенки 0b00000100. Почти все операции будут выглядеть так же, но в правом верхнем углу мы получим:
Выставим все значения по периметру:

Псевдокод для выставления начальных стенок:
При выводе на экран через консоль эти значения будут представлены в десятичной системе счисления, поэтому не пугайтесь, если увидите такое:
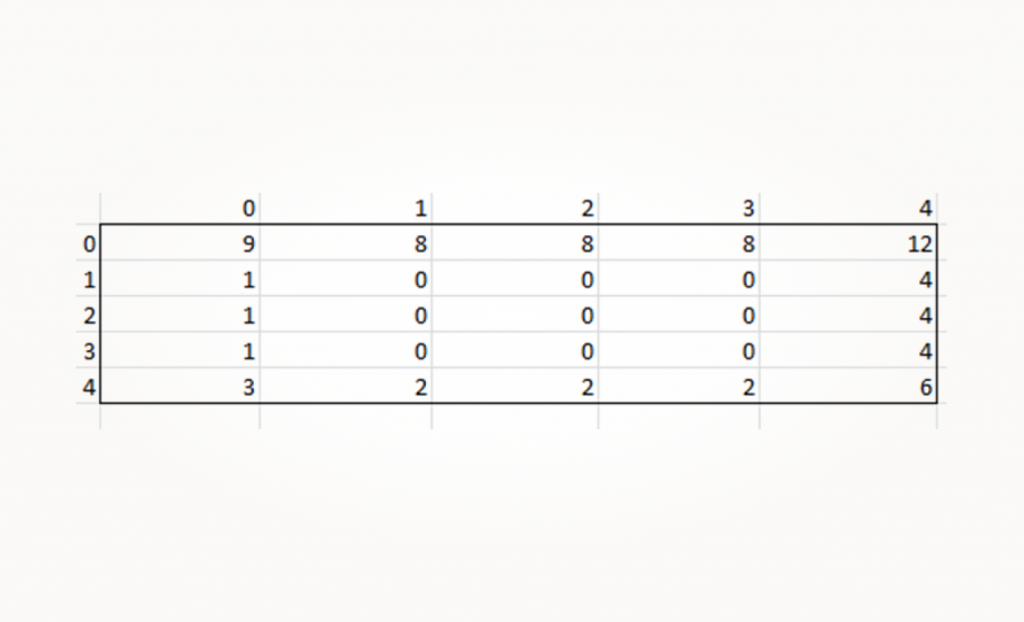
Обновление карты при движении робота
Рассмотрим, как робот будет собирать информацию о карте при движении. Предположим, что он находится в ячейке (4, 0) и повернут вверх.
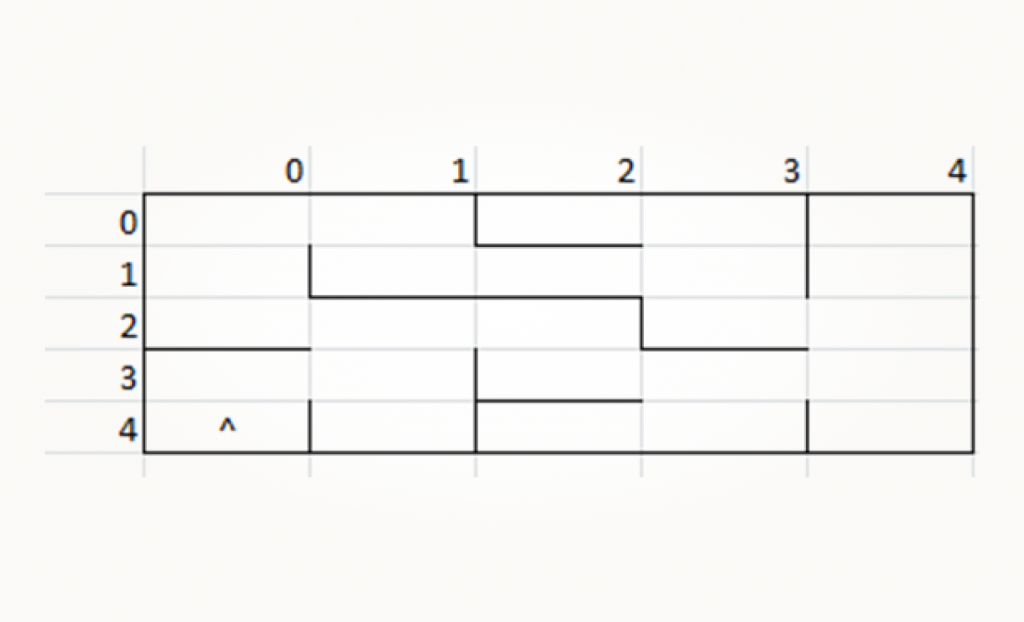
В этой позиции робот видит две стенки, правую и левую. Это соответствует маскам right_wall (0b00000100) и left_wall (0b00000001). Теперь нам нужно добавить эти биты к нашей карте. Как и при выставлении внешних стен, мы продолжаем пользоваться операцией ИЛИ.

В этой ячейке мы уже предварительно получили 0b00000011, зафиксировав внешние стенки лабиринта снизу и слева. Теперь добавим правую:
Если теперь второй раз добавить левую стенку, результат не изменится, поскольку мы это уже делали:
В виде псевдокода получаем:
Теперь наша карта выглядит так:

Далее робот решает ехать прямо и перемещается в ячейку (3, 0).
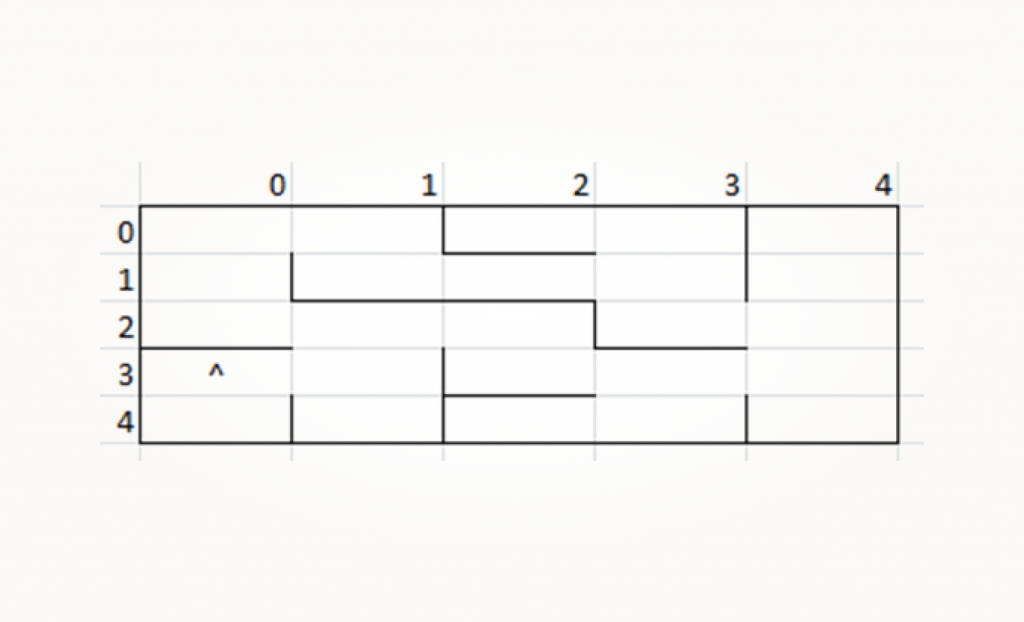
Сенсоры определяют наличие стен спереди и слева. Текущее значение в этой ячейке 0b00000001. Берем маски up_wall и left_wall, выполняем битовые операции с ними — то есть с 0b00001000 и 0b00000001. Получаем 0b00001001.
Следующим движением роботу нужно будет проехать одну ячейку вправо.
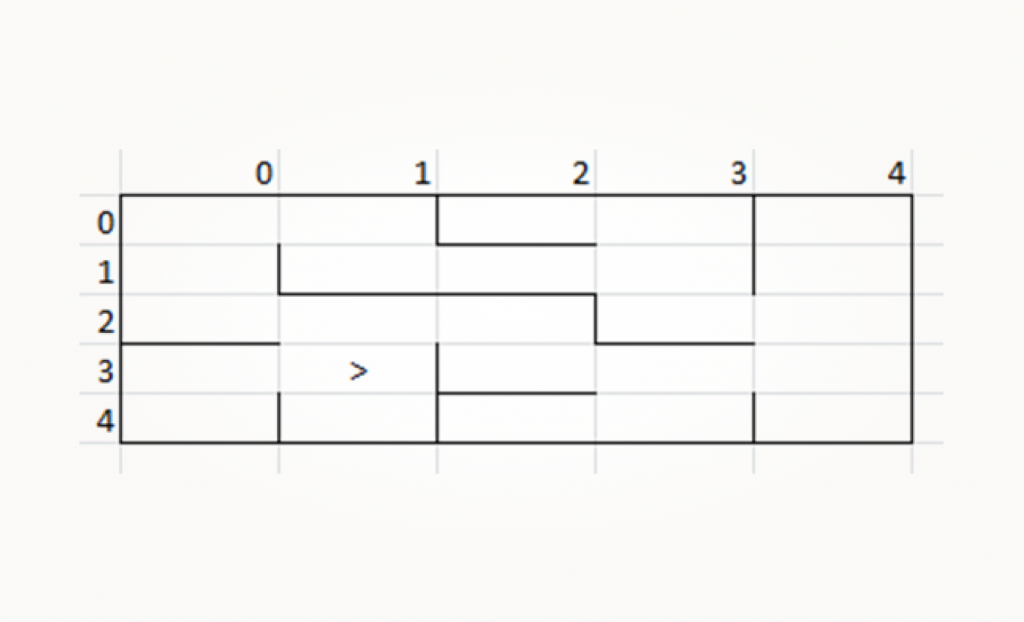
Робот повернулся относительно карты, и теперь датчики будут обнаруживать стенки с других позиций. Левый датчик не смотрит на левую по умолчанию стенку, передний не смотрит на верхнюю и так далее. Поэтому важно отслеживать не только ячейку робота, но и его направление.
Для текущей позиции маской левой стенки относительно робота будет up_wall, передней стенки — right_wall и правой стенки — down_wall. Здесь обнаружена только стенка спереди, так что выставляем только это значение:
Далее робот решил переместиться на клетку вниз, и его позиция выглядит так:
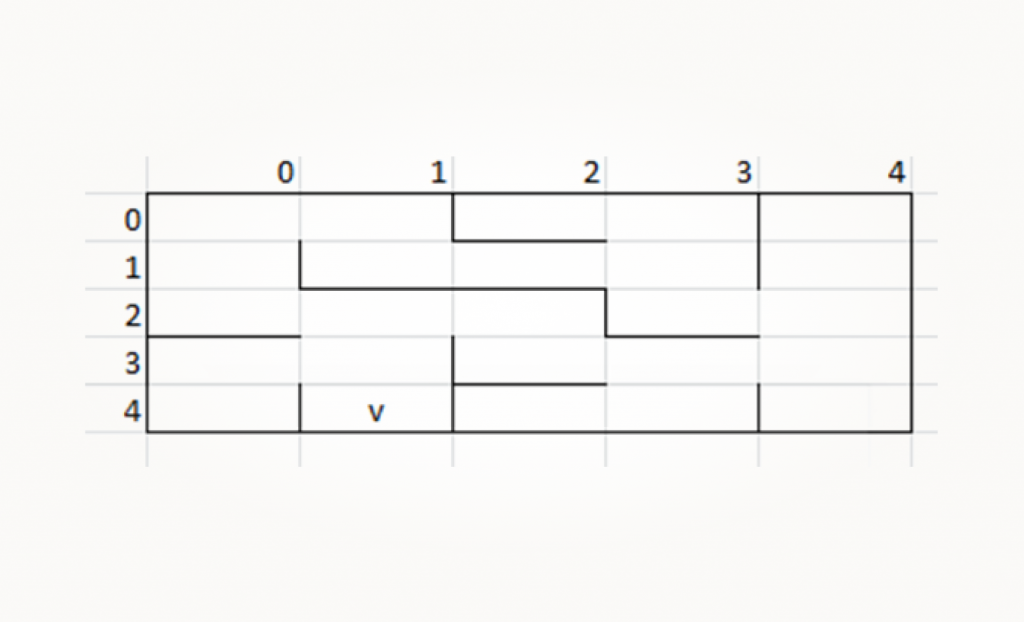
С учетом позиции робота нам понадобятся маски right_wall для левого, down_wall для переднего и left_wall для правого датчика. Все три стенки зафиксированы роботом, так что мы получаем выражение:
И напоследок еще один возможный случай: робот доехал до ячейки (4, 2) и смотрит влево.
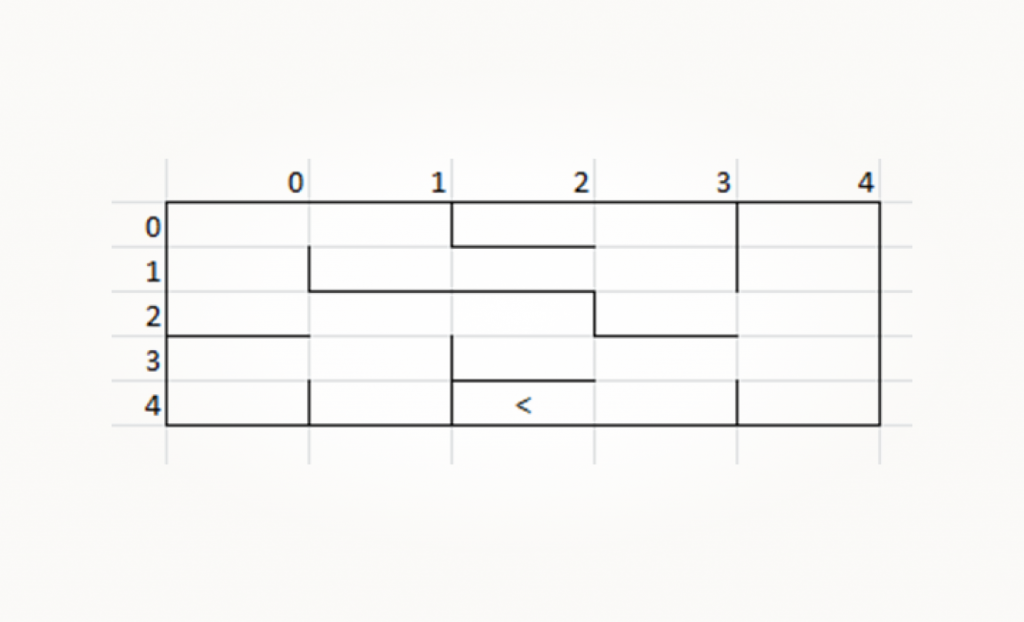
Здесь нам нужны будут маски down_wall, left_wall и up_wall. Получаем следующее выражение:
В виде псевдокода выставление стен на карте будет выглядеть так:
Отслеживание направления робота
Из примеров выше видно, что направление робота — это важная часть алгоритма составления карты. Для описания здесь можно использовать одну целочисленную переменную, которая принимает четыре значения: 0 (вверх), 1 (вправо), 2 (вниз) и 3 (влево). Для управления полезно иметь функцию, которая изменяет направление робота в зависимости от его действий.
Проверка стен на карте
Как убедиться, есть ли на карте какая-либо известная нам стенка? Проверить нужный бит в ячейке мы можем через операцию битового И. Возьмем для примера ячейку с координатами (4, 2):

Предположим, что в ней робот смотрит влево (direction = 3):
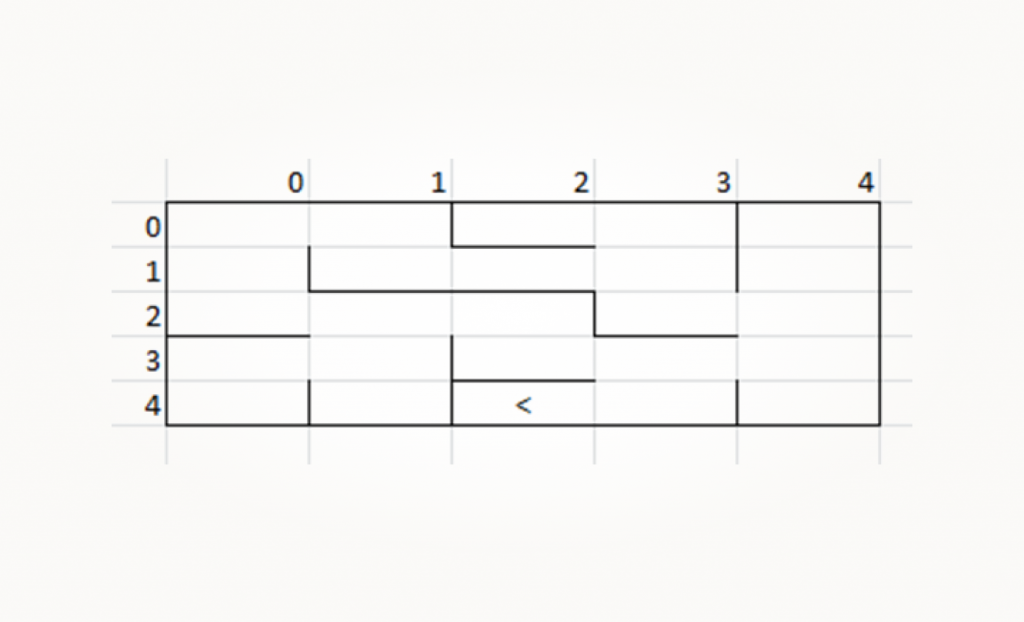
В этой ячейке были определены три стенки: верхняя, нижняя и левая. Пусть алгоритм робота велит ему повернуть направо. Как понять, есть ли стенка справа от робота?
Мы знаем, что для робота правая стенка является верхней в ячейке, поэтому берем соответствующую маску up_wall. Применим операцию И:
Чтобы проверить метод, проигнорируем положение робота и подставим маску right_wall:
Наш метод работает: применяя операцию побитового И к значению ячейки и маске, мы можем определить, записывали ли мы маску для стенки или нет.
Теперь мы можем добавить еще 3 функции, которые позволят нам проверять стенки слева, спереди и справа от робота. Рассмотрим псевдокод одной из этих функций.
Передвижение робота
С картой разобрались, осталось научить робота передвигаться относительно лабиринта, который построен в его памяти. Как изменяется направление, мы уже рассмотрели. Теперь будем изменять координаты робота — научим реагировать на команду «пройди одну ячейку вперед».
Это реализуется через простые операции с вычитанием и прибавлением индексов. Когда робот движется по карте наверх, каждую ячейку его координата y уменьшается на 1, при движении вправо увеличивается на 1 координата х и наоборот. Вот как будет выглядеть наша функция:
Пример алгоритма исследования лабиринта
Теперь у нас есть все компоненты, чтобы построить карту реального лабиринта и затем проверять стенки при помощи этой карты. Рассмотрим простой алгоритм исследования лабиринта на основе правила левой руки. Это значит, что робот сначала пытается проехать одну ячейку влево, если там нет стенки. В противном случае он пробует другие направления, последовательно поворачивая на 90 градусов по часовой стрелке. Если за три такие попытки он определяет рядом стенку, то разворачивается и едет обратно.
Предположим, что наш робот физически умеет:
- проезжать одну клетку вперед при помощи функции forward (),
- поворачивать налево при помощи turn_left (),
- поворачивать направо через turn_right (),
- считывать показания с левого, переднего и правого датчика при помощи get_left_wall (), get_front_wall () и get_right_wall () соответственно.
Тогда наш алгоритм будет выглядеть так:
Этот алгоритм позволит построить полную карту лабиринта, если этот лабиринт содержит лишь один путь от старта до финиша, чтобы в дальнейшем искать по этой карте короткий путь от начальной точки до конечной. Использование функций check_left_wall () и ей подобных здесь избыточно, так как мы можем просто взять только что полученные данные с датчиков. Я вставил их здесь исключительно ради демонстрации работы рассмотренных алгоритмов. В реальных соревнованиях Micromouse путей много и алгоритм несколько иной.
Упрощение функций
В предыдущих разделах мы научили робота строить карту. Далее будет немного материала для «продвинутых пользователей».
Сейчас все функции содержат очень много условий, которые могут быть упрощены при помощи модульной арифметики. В большинстве случаев нам потребуется модульная арифметика по модулю 4, так как у нас четыре направления.
На примере модуля 4 и будет идти дальнейшее объяснение. У нас есть переменная, которая отвечает за направление, и одно фиксированное значение для каждого из четырех направлений. Посмотрим внимательнее, как изменяются эти значения при поворотах.
Начнем с поворотов направо. Робот при старте смотрит наверх, то есть direction = 0. Далее робот повернет направо — мы фиксируем за этим направлением значение 1. После этого робот ещё раз повернет направо: direction = 2. Несложно заметить, что после каждого поворота направо мы увеличиваем значение direction на 1.Но что делать, если робот смотрел налево (direction = 3) и затем повернул направо? Мы получаем значение 4, хотя хотелось бы иметь 0. Что, если робот продолжит поворачивать направо? Мы будем получать значения 5, 6, 7 и так далее. Посмотрим, как эти значения сопоставляются с теми, которые нам нужны.
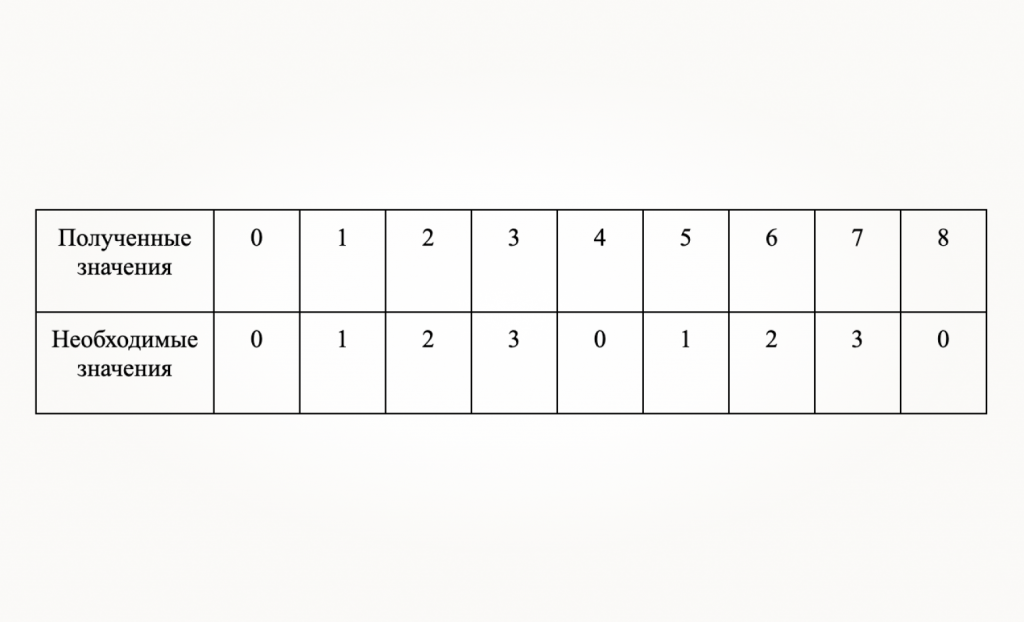
Необходимые значения — это не что иное, как остаток от деления полученных значений на 4. Если робот смотрел налево и повернул направо, то мы получили direction = 4. Остаток от деления 4 на 4 равен 0, что соответствует направлению вверх. В большинстве языков программирования для получения остатка используется оператор деления по модулю, вызываемый через символ %. В итоге поворот направо мы можем записать так:
В таком случае нам даже не нужно знать, в какую сторону смотрел робот до поворота.
Теперь о поворотах налево. Представим, что робот смотрит влево (direction = 3). При повороте налево мы получим значение 2, затем 1, затем 0. После значения 0 пойдут отрицательные числа, и магия с остатком от деления здесь с ходу не заработает. Попробуем построить таблицу для первых трех отрицательных чисел. Этого достаточно, так как мы уже выяснили, что у нас циклически повторяется только 4 значения.
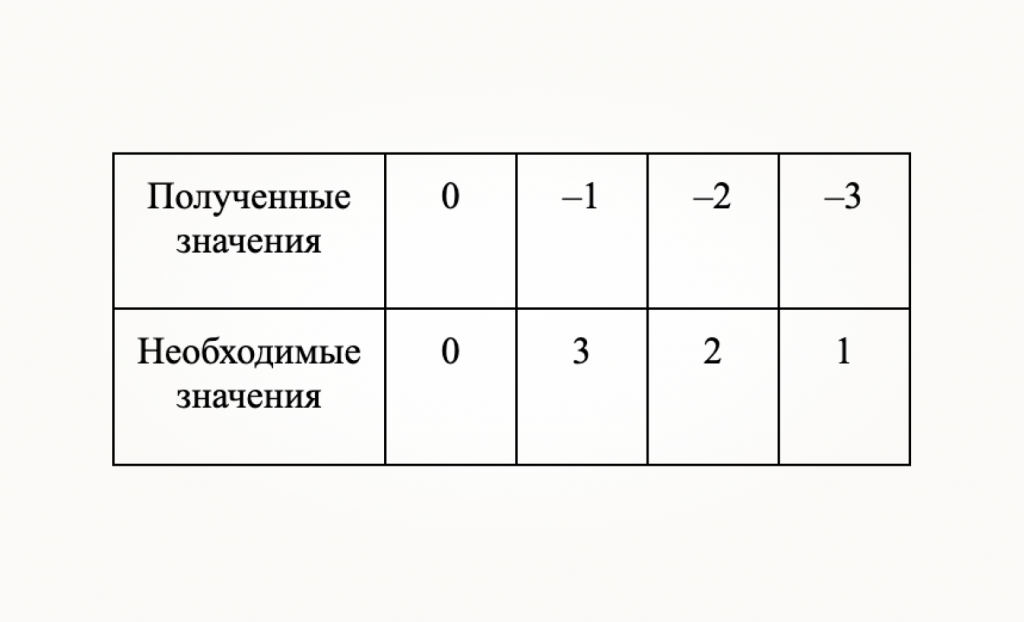
Можно заметить, что нужные нам значения отличаются ровно на наш модуль (4). Запишем формулу поворота налево:
Если робот находится в позиции 0 («смотри вверх») и поворачивает налево, мы получаем direction = (0 — 1 + 4) % 4 = 3, что соответствует значению «смотрит налево». Расчет значений для других направлений тоже никак не изменился, поскольку мы прибавляем значение модуля (4% 4 = 0).
Упростим выражение:
Интересно, что для поворота направо и налево мы используем глобальные значения этих состояний — 1 и 3 соответственно. Вернемся к функции изменения направления и перепишем ее:
При помощи модульной арифметики у нас получилось сократить количество строк этой функции с 28 до одной. Другие рассмотренные функции (set_walls, check_left_wall, check_front_wall и check_right_wall) также могут быть упрощены, с помощью модульной арифметики и нескольких дополнительных массивов, например массива всех масок:
Оптимизация выставления стенок
Последнее, что мы рассмотрим здесь, — это оптимизация построения стенок на карте робота. Представим начальную позицию робота и карту описанных им стенок:


Когда мы выставляем значение правой стенки в текущей ячейке, мы можем выставить и значение левой стенки в соседней. То есть после первого обновления стенки у нас поменяется не только значение ячейки (4, 0), но и значение ячейки (4, 1). Учтем только, что в соседней ячейке нам нужно будет выставить стенку в противоположном направлении, то есть позиция бита будет отличаться на 2. В итоге после первого обновления карта будет выглядеть следующим образом:






Денис, здравствуйте!
Вы пишете «робот принимает решение двигаться в таком-то направлении». А как именно он принимает это решение? Это очень интересно, а Вы об этом ничего не говорите.